sktimeで時系列データを予測してみた

sktimeとは

sktimeは時系列に特化した機械学習のためのライブラリです。

時系列問題の予測・分類についてのアルゴリズムやその構築・チューニング評価するためのツールが含まれます。

またインターフェースはsklearnを踏襲しており、sklearnとの組み合わせても使用することが可能です。

今回はこちらを使って時系列データの予測をやってみました。

モジュールのインポート

import numpy as np
from sktime.datasets import load_airline
from sktime.forecasting.compose import make_reduction
from sklearn.ensemble import RandomForestRegressor
from sktime.forecasting.model_selection import temporal_train_test_split
from sktime.performance_metrics.forecasting import MeanAbsolutePercentageError
import pandas as pd
import matplotlib.pyplot as plt

サンプルデータのロード

sktimeに含まれるairlineデータセットを使います。

こちらは、定番のBox & Jenkinsの航空会社データで、1949年から1960年の各月毎の乗客数のデータとなります。

y = load_airline()
print(y)

Period
1949-01    112.0
1949-02    118.0
1949-03    132.0
1949-04    129.0
1949-05    121.0
           ...  
1960-08    606.0
1960-09    508.0
1960-10    461.0
1960-11    390.0
1960-12    432.0
Freq: M, Name: Number of airline passengers, Length: 144, dtype: float64

どのようなデータか、プロットしてみましょう。

fig = plt.figure(figsize=(15, 8), dpi=50)
ax1 = plt.axes()
ax1.plot(y.values)

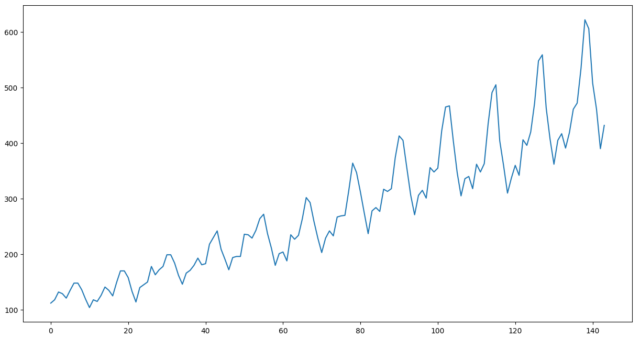
トレンドと周期性を持ったデータであることがわかります。

次に、temporal_train_test_splitにより、時系列を考慮したデータ分割を行います。

• この処理は実際は時系列を考慮するのではなく、先頭側をtrain、末尾側をtestにするだけですので、あらかじめ時系列順にソートされている必要があります。
• デフォルトの場合はtrain:test=3:1で分割されます。

y_train, y_test = temporal_train_test_split(y)

モデル構築と学習

regressorを指定して時系列問題を解かせます。

• regressorはsklearnにある回帰モデルを指定することが可能です。
• sktimeのチュートリアル通りにまずはRandomForestRegressorを使ってみます。
• 窓長window_lengthを指定することで、入力範囲を指定できます。

regressor = RandomForestRegressor()
forecaster = make_reduction(
    regressor,
    strategy="recursive",
    window_length=12,
    scitype="infer",
)
forecaster.fit(y_train)

推論

predictにindexを与えることで推論が可能です。

fh = np.arange(1, len(y_test) + 1)  # forecasting horizon
y_pred = forecaster.predict(fh)

評価

評価指標としてMAPE導出します。

• MAPEは正解値と予測値の差を正解値でわったもの絶対値に、100をかけた(パーセント化)したものの平均です。

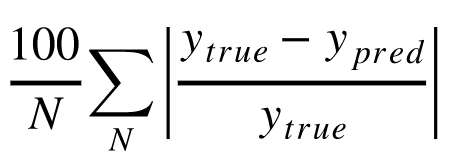
• 正解値で割ることにより、ずれをパーセントで説明することができるメリットがあります。
• 一方、正解値が小さい場合には値が大きくなってしまうため注意が必要です。

mape = MeanAbsolutePercentageError()
print(f"mape = {mape(y_test, y_pred)}")

mape = 0.12726220177918104

これは実際にどの程度の性能でしょうか？

グラフに描画して確認します。(オレンジが予測値です)

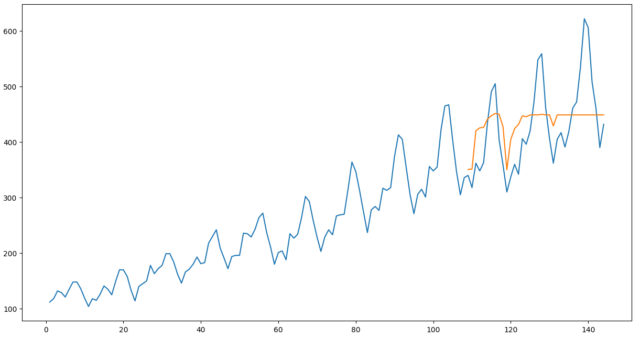
直線となっている部分もあり、誤差が大きいように見えます。

時系列に特化した回帰モデルを使っていないということが原因となっている可能性があります。

より高度なアルゴリズム１：ARIMAモデル

代表的なアルゴリズムであるARIMAを使ってみます。

ARIMAは1976年にBox & Jenkinsにより提案された古典的な手法ですが、時系列問題には非常にマッチした手法です。

簡単に理論を説明します。

ARモデル

まず最初にARモデル(自己回帰モデル)を考えます。

ARモデルは過去の出力データと現在の入力を使って、現在の出力を推定するモデルです。

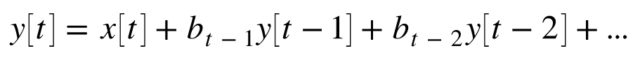
次数pでどの程度過去のデータを使うか決定し、p=1の場合は、y[t-1]のデータまでを使用します。

MAモデル

次にMAモデル(移動平均モデル)です。

MAモデルは、過去の入力データと現在の入力データを使って、現在の出力を推定するモデルです。

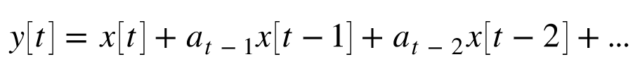
次数qでどの程度過去のデータを使うかを決定し、q=1の場合は、x[t-1]のデータまでを使用します。

ARMAモデル

ARMAモデルは、ARモデルとMAモデルを組み合わせたものです。

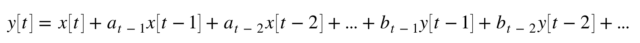
組み合わせることによってより一般的な定常特性をモデル化できます。

ARIMAモデル

ARMAモデルまでは、定常的な特性をもった時系列データが前提です。

しかし実際は今回使用している乗客数のデータなど長期的なトレンドを有した非定常的な特性をもつ時系列データがあります。

こういった場合にモデル化する対象を差分信号とすることで、トレンドを持つ時系列データをモデル化します。

具体的には、1階の階差行列を使う場合は、以下をモデル化対象とします。

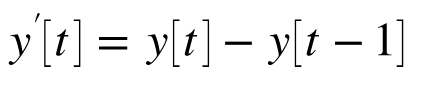
このy'[t]をARMAモデルでモデル化します。(もちろんその際にARの部分に使う出力はy'[t-1]などを使います)

実際にはこの階数はパラメータnであり、最適な階数を求める必要があります。

実際にARIMAを使ってみた

sktimeでARIMAを使うには、pmdarimaを追加でインストールする必要があります。

pmdarimaは、Rの時系列解析で有名なforecastの中にあるアルゴリズムを移植したものです。

poetry add pmdarima # pipなどでも可能

学習、推論、評価を同時に実行します。

from sktime.forecasting.arima import ARIMA

forecaster = ARIMA(
    order=(1, 1, 0),
    seasonal_order=(0, 1, 0, 12),
    suppress_warnings=True)
forecaster.fit(y_train)

y_pred = forecaster.predict(fh)

mape = MeanAbsolutePercentageError())
print(f"mape = {mape(y_test, y_pred)}")

fig = plt.figure(figsize=(15, 8), dpi=50)
ax1 = plt.axes()
ax1.plot(np.arange(1, len(y) + 1), y.values)
ax1.plot(np.arange(len(y_train)+1, len(y) + 1), y_pred.values)

mape = 0.04257105708811475

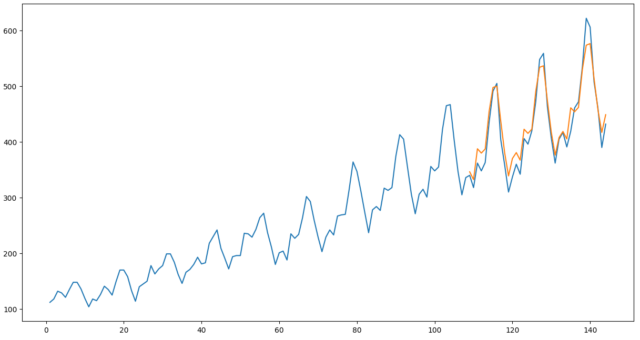
MAPEが改善し、グラフとしてもかなり改善していることがわかります。

３番目のピーク時に誤差が大きくなる点が少し気になるところです。

ARIMAのパラメータ自動検索

ARIMAにはフィルタ次数(p,q)や階数(n)などのパラメータがありますが、これを自動探索するAutoARIMAという機能もあります。

これもRのforecastからpmdarimaに移植されていますので試してみましょう。

from sktime.forecasting.arima import AutoARIMA
forecaster = AutoARIMA(sp=12, d=None, max_p=10, max_q=10, suppress_warnings=True)
forecaster.fit(y_train)

y_pred = forecaster.predict(fh)

mape = MeanAbsolutePercentageError()
print(f"mape = {mape(y_test, y_pred)}")

fig = plt.figure(figsize=(15, 8), dpi=50)
ax1 = plt.axes()
ax1.plot(np.arange(1, len(y) + 1), y.values)
ax1.plot(np.arange(len(y_train)+1, len(y) + 1), y_pred.values)

mape = 0.04117062367043446

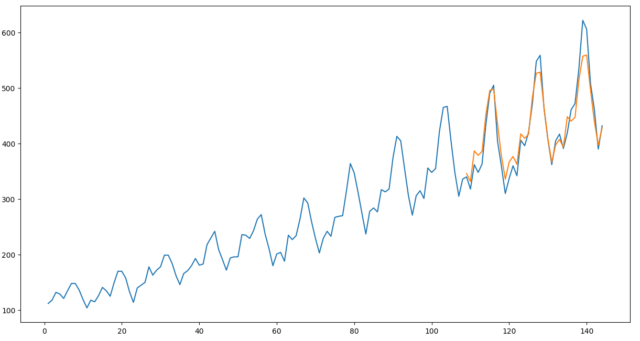
グラフ上は違いが判りませんが、少しだけMAPEは改善しています。

より高度なアルゴリズム２：Prophet

ProphetはFacebookにより開発されたアルゴリズムです。

こちらの記事にわかりやすい解説がありますのでここでは割愛します。

• https://devblog.thebase.in/entry/2019/12/20/110000_1

sktimeでProphetを使うには、prophetを追加でインストールする必要があります。

poetry add prophet # pipなどでも可能

また注意点として、入力するSeriesのIndexをDatetimeIndexにしておく必要があります。

(datasetのままだと、PeriodIndexとなっています)

y_train_pp = y_train.to_timestamp(freq="M")
y_train_pp.head(10)

1949-01-31    112.0
1949-02-28    118.0
1949-03-31    132.0
1949-04-30    129.0
1949-05-31    121.0
1949-06-30    135.0
1949-07-31    148.0
1949-08-31    148.0
1949-09-30    136.0
1949-10-31    119.0
Freq: M, Name: Number of airline passengers, dtype: float64

学習、推論、評価を同時に実行します。

from sktime.forecasting.fbprophet import Prophet

forecaster = Prophet(
    seasonality_mode='multiplicative',
    n_changepoints=int(len(y) / 12),
    add_country_holidays={'country_name': 'Germany'},
    yearly_seasonality=True)
forecaster.fit(y_train_pp)

y_pred = forecaster.predict(fh)

mape = MeanAbsolutePercentageError()
print(f"mape = {mape(y_test, y_pred)}")

fig = plt.figure(figsize=(15, 8), dpi=50)
ax1 = plt.axes()
ax1.plot(np.arange(1, len(y) + 1), y.values)
ax1.plot(np.arange(len(y_train)+1, len(y) + 1), y_pred.values)

mape = 0.07233720490928143

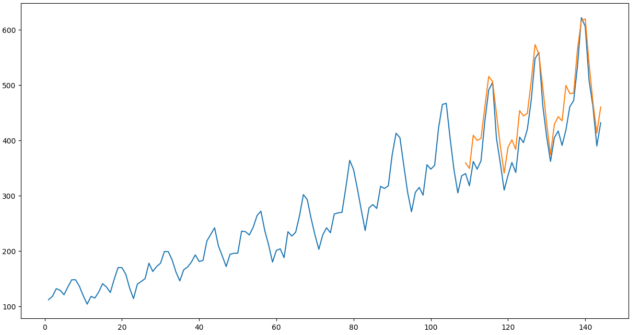
MAPEでは、ARIMAに及ばないのですが、ピーク時の誤差が少ない傾向となりました。

もう少し調整を行ったり、用途によってARIMAと使い分けた方が良い可能性がありそうです。

まとめ

いかがでしたでしょうか。

このほかにも、Javaのtsmlツールキットから移植された時系列の分類・回帰問題の最先端のアルゴリズムが使えるようです。

sklearnと同様、pipeline化することなども可能ですので、様々な時系列解析を試す際に有用と思いました。