
【セッションレポート】 ゲームプログラマのための数学の歩き方 - 連続最適化編 #CEDEC2025
登壇者: 長谷川 勇 (株式会社スクウェア・エニックス)、前田 航希 (九州大学)、鍛冶 静雄 (九州大学/京都大学)、落合 啓之 (九州大学)
日時: 2025 年 7 月 24 日 (木) 16:40 ~ 17:40
会場: CEDEC2025 第 6 会場
カテゴリ: AC (学術研究) | チュートリアル | 公募
概要
本セッションでは、ゲーム開発に携わるプログラマに向けて、連続最適化 (continuous optimization) の基礎理論とその応用例が紹介されました。近年、機械学習や物理シミュレーション、アニメーション制御など、ゲーム制作のさまざまな分野で最適化手法の重要性が高まっています。特に連続最適化は、連続量を扱う問題に対して柔軟かつ効果的に解を導く手法として注目されています。
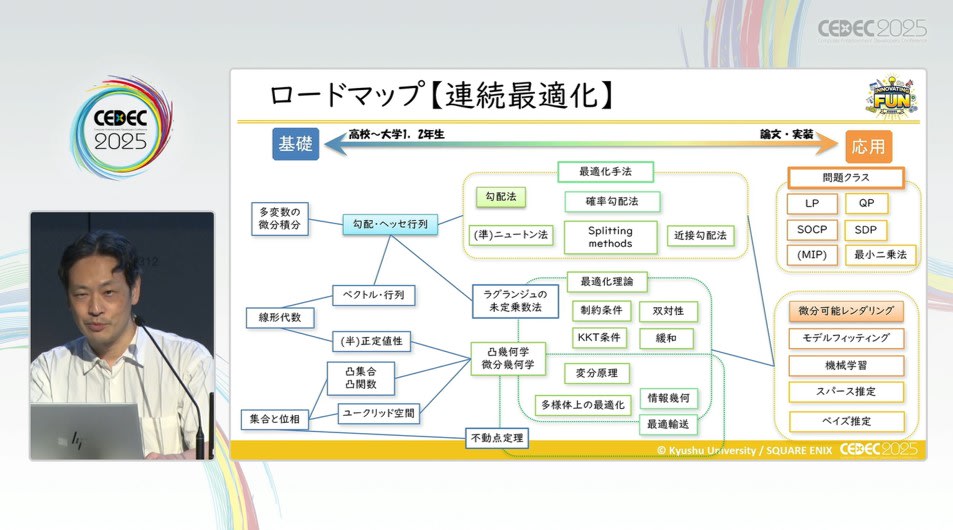
講演は CEDEC2020 から継続して行われている「数学の歩き方」シリーズの一環ですが、内容は独立しており、前提知識がなくても理解ができる構成です。数学が得意でない開発者でも直感的に内容を捉えられるよう、概念や用語の解説には図解や実例が多く使われており、学術的な厳密さよりも、現場での実践を重視した構成となっていました。
最適化問題を理解する
最適化問題とは、ある目的関数の値を最小化または最大化するために、変数の値を調整する課題のことです。たとえば、キャラクターの移動経路を最短にしたい、画像の見た目をできるだけ自然に変化させたい、といった場面では、目的に応じたスコア関数を定義し、それを最適化する必要があります。
最適化には大きく分けて 離散最適化 と 連続最適化 の 2 種類があります。前者は「選ぶ」問題、つまり有限個の選択肢から最適なものを探すのに向いており、後者は「調整する」問題、すなわち連続的に変化するパラメータを対象とします。本セッションで扱われたのは後者です。
連続最適化では、目的関数の形が滑らかであればあるほど、微分や勾配といった数学的性質を活用できます。特に、目的関数の勾配(つまり、どの方向に値が増えるか)を利用して、より良い値へと変数を少しずつ更新する 勾配降下法 (gradient descent) は、もっとも基本的かつ広く使われている手法です。

勾配降下法を改良した手法として、モーメンタム法 や Adam、確率的勾配降下法 (SGD) なども紹介されました。これらは、学習速度の調整や収束の安定化といった課題に対処するために使われます。形状合わせなどの文脈で利用される 反復最近点法 (ICP: Iterative Closest Point) も、実用的な連続最適化アルゴリズムの例として紹介されました。
こうした手法に共通するのは、目的関数を定義したうえで、その最適値を求めるという点です。これにより、さまざまな分野の問題を数理モデルとして扱うことが可能になります。たとえば、キャラクターの動き、カメラの配置、光の当たり方など、直感的には異なる課題も、すべて「目的を定めて変数を調整する」問題に置き換えることができます。
ゲーム開発に応用する
連続最適化は、ゲーム開発のさまざまな分野に応用されています。本セッションでは、特に次のようなユースケースが紹介されました。
- 物理シミュレーションやアニメーション制御
キャラクターの自然な歩行モーションや関節の動きを生成する際に、目的の動作に近づけるよう関節角度などのパラメータを調整する必要があります。このとき、目的関数を定義し、その最小値を探すという形で連続最適化が活用されます。

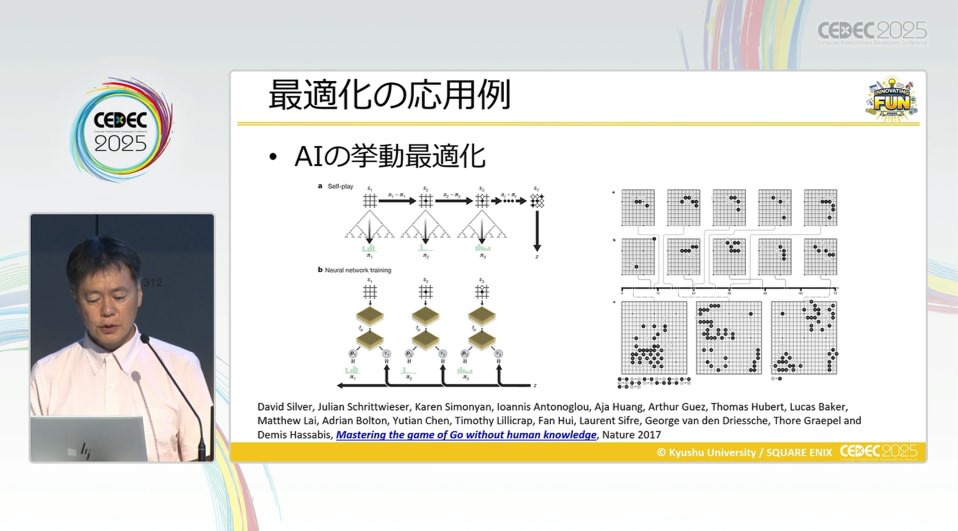
- AI の行動最適化
特定の条件下で効率よく移動する経路や、戦術的な判断を導き出すパラメータを調整する際に、強化学習と組み合わせて連続最適化が使われることがあります。特に、ロジスティック回帰のように 0〜1 の連続値として出力を設計することで、学習過程の安定性が向上するという話題にも触れられていました。
- レンダリングにおける逆問題
「画像の右下を暗く見せたい」などのビジュアル的な目的を達成するために、光源やマテリアルの設定をどのように変更すればよいかを逆算するタスクです。こうした問題では、目的関数を定義した上で、変更すべきパラメータをスコアリングし、連続最適化によってその最適解を導きます。
このような応用を可能にするには、自動微分機能を持つライブラリの存在が重要です。セッション内では、微分可能レンダラーなど一部のライブラリが紹介されました。これにより、開発者は複雑な微分計算を自前で用意せずに済み、実装の負担が軽減されます。
実務に役立つ知識として、双対問題の活用も挙げられました。最適化の計算においては、元の問題をそのまま解くよりも、双対問題に変換した方が計算効率が良くなる場合があります。ただし、これはケースバイケースであり、すべての問題に適用できるわけではないことも明言されました。
微分可能シミュレーションの応用例として、MRI から血流を推定するタスクなど、ゲーム以外の分野への応用も紹介されました。
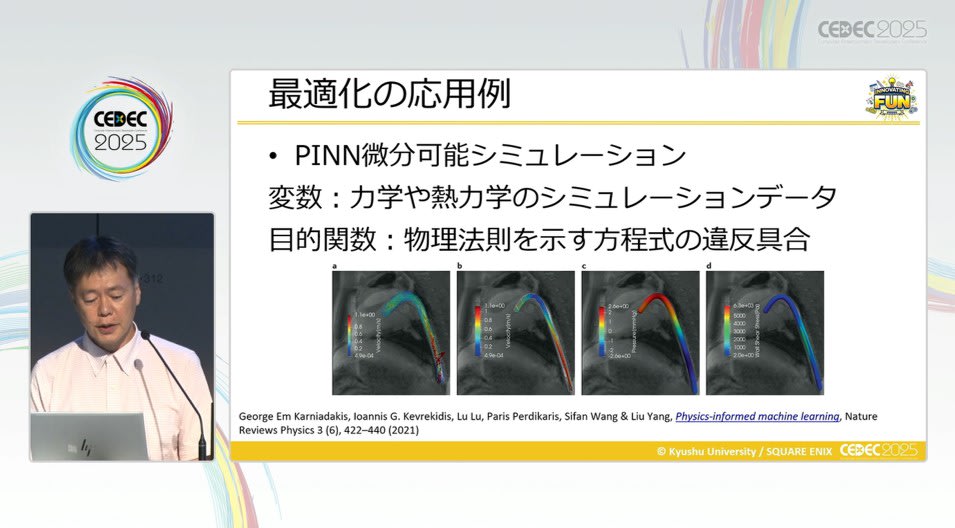
このように、連続最適化はゲームに限らず幅広い領域で有用であり、目的関数をどう定義するか、どの手法を選ぶか、そしてツールをどう活用するかが実装の鍵になります。
まとめ
連続最適化は、機械学習や物理シミュレーション、レンダリングの逆問題といった、ゲーム開発の中でも数値的に連続な処理が求められる領域において重要な役割を果たします。本セッションでは、勾配降下法をはじめとした最適化手法の基本から、実際のゲーム開発における応用可能性までが幅広く紹介されました。特に、勾配ベースの手法を支える自動微分の活用や、微分可能レンダラーの存在は、最適化を技術的な抽象概念にとどめず、実装可能なアプローチとして扱うための鍵となります。
連続最適化は、ただ計算技術として学ぶのではなく、実際の課題をどのようにモデル化し、どのように最適化に落とし込むかという視点で捉えることが重要です。ゲーム開発者にとっても、これらの考え方を知っておくことは、より柔軟で現実的な問題解決につながる手がかりとなるでしょう。








