
Classmethod AI Talks(CATs) #6 「Qdrantでベクトルデータベースに入門してみよう」というタイトルで登壇しました #catalks
この記事は公開されてから1年以上経過しています。情報が古い可能性がありますので、ご注意ください。
リテールアプリ共創部@大阪の岩田です。
2024/10/30(水)に開催されたClassmethod AI Talks(CATs) #6 生成AIサービス開発の実践 - 周辺技術を基礎から応用までキャッチアップ!にて「Qdrantでベクトルデータベースに入門してみよう」というタイトルで登壇させていただきました。
このブログでは登壇内容をかいつまんで紹介させていただきます。
ベクトルデータベースとは
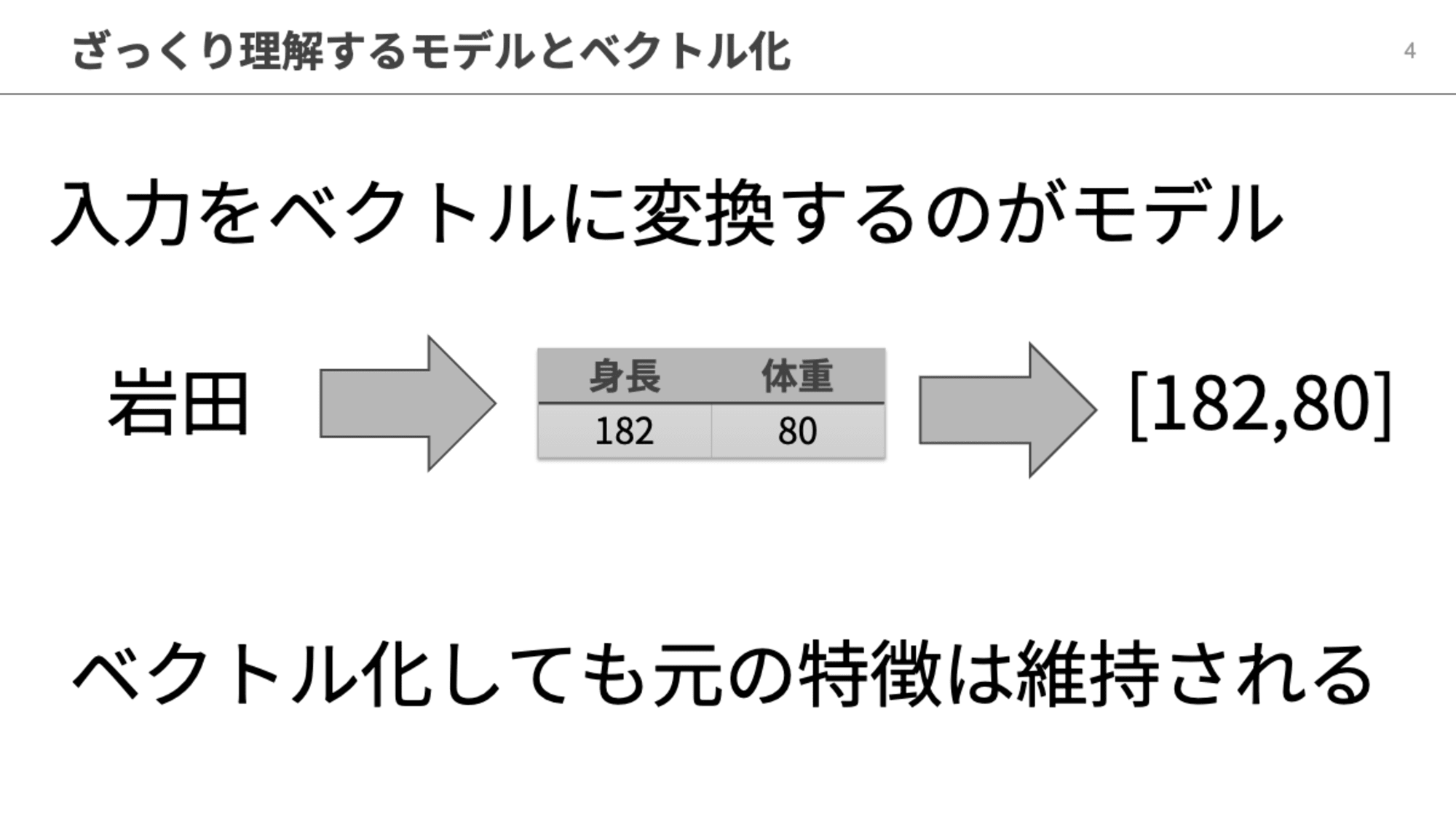
ベクトルデータベースはベクトルデータの格納や検索に特化したデータベースで、意味的に近しいデータを検索できるのが特徴です。ベクトルデータベース自体は昔からある技術ですが、生成AIの流行と共に注目度が上がっている技術です。

Qdrantの概要
QdrantはOSSのベクトルデータベースです。Qdrantの概要については以下のブログが参考になります。
Dockerで簡単に起動できる、Web UIを備えているといった特徴からベクトルデータベースの入門にオススメなデータベースです。
Qdrantで利用可能な指標
ベクトルデータベースを利用すると検索条件に指定したデータと意味的に近しいデータが検索できるのですが、この「意味的に近しい」というのはどういうことでしょうか?この類似度を表す指標がいくつかあり、Qdrantでは4つの指標が利用可能です。これらの指標をユースケースに合わせて使い分けることが重要です。
各指標について詳細を説明していきます。
ドット積
まずドット積です。こちらはベクトルの内積を用いた指標です。

Qdrantのソースコードでいうとこの辺りに実装されています。
※この指標は正規化されたデータに対して使う指標なので、この計算例は本来良くない例です。
コサイン類似度
続いてベクトル同士のコサイン値を用いた指標であるコサイン類似度です。

計算ロジックはこの辺り。
前処理を行ってからドット積を計算するような流れになります。
ユークリッド距離
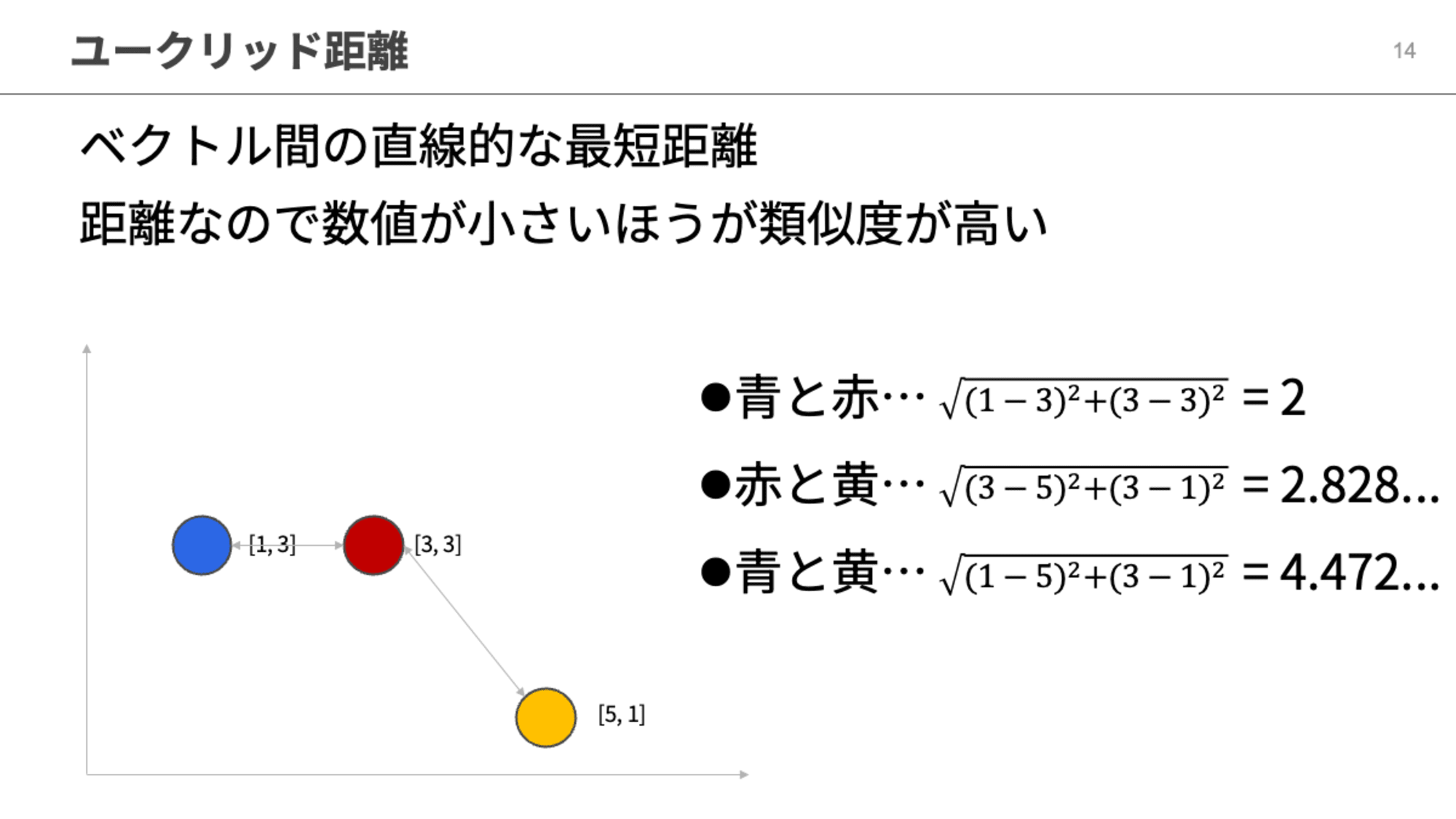
次はベクトル間の直線的な最短距離を利用するユークリッド距離です。
ドット積とコサイン類似度は計算結果の数値が大きいほど類似しているという指標でしたが、ユークリッド距離と後述するマンハッタン距離は「距離」を用いた指標なので計算結果が小さいほど類似していることになります。
計算ロジックはこの辺り。
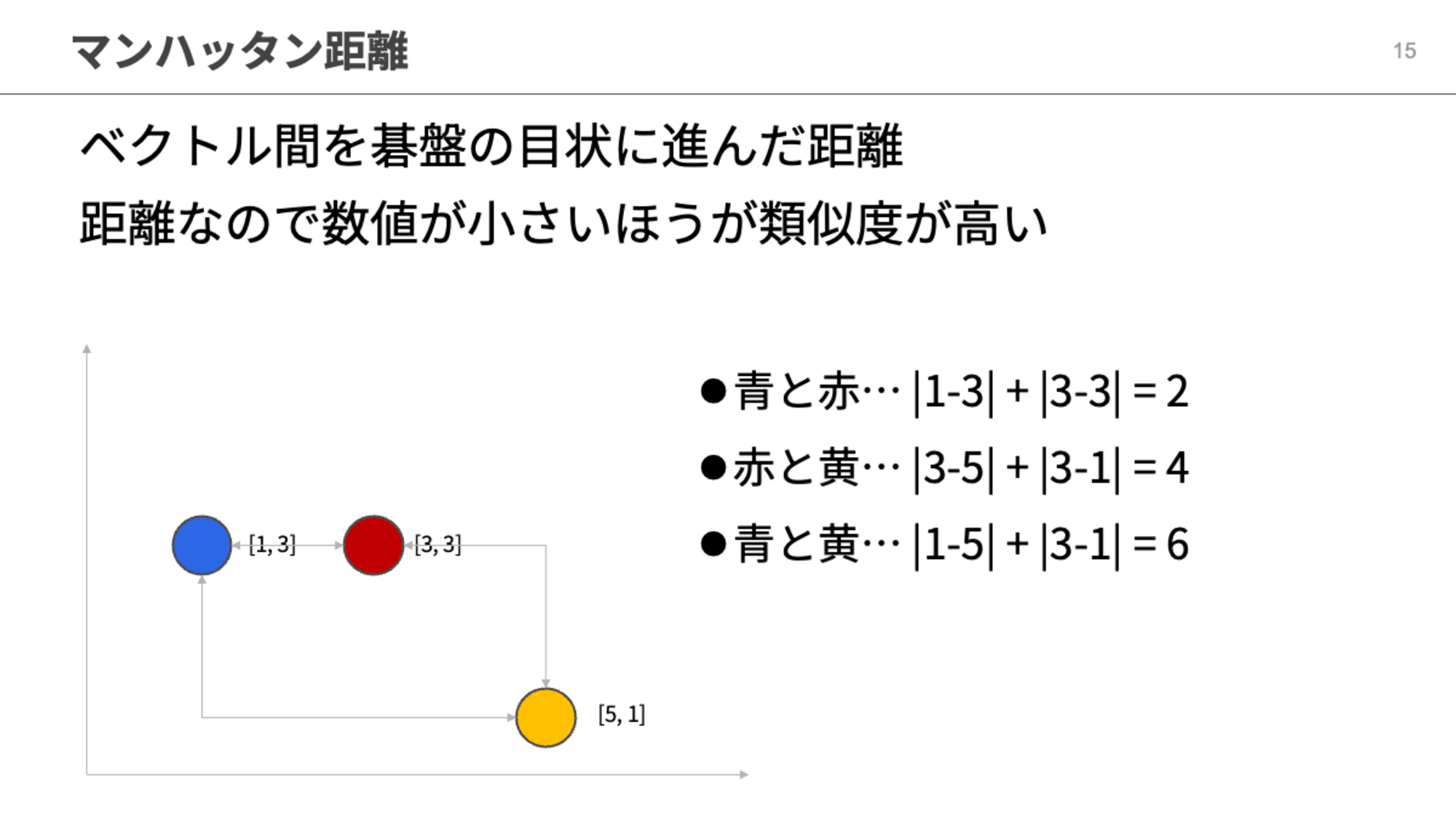
マンハッタン距離
最後にマンハッタン距離です。将棋の飛車のようなイメージですね。
計算ロジックはこの辺り。
ベクトルの種類
ベクトルには密ベクトルと疎ベクトルの2種類があります。どちらが優れているというものではなく、それぞれメリット・デメリットがあるので、要件に応じた適切なベクトルを利用することが重要です。

Hybrid Search
ベクトルには密ベクトルと疎ベクトルがあるという話をしましたが、1つのポイントでこれらのベクトルを併用可能です。ポイント:ベクトルは1:1ではなく1:Nということですね。
また、密・疎ベクトルに限らず、マンハッタン距離を利用するベクトルとユークリッド距離を利用するベクトル両方を1つのポイントに登録するといった使い方も可能です。
1つのポイントに対して複数のベクトルを登録した場合は各ベクトルに対してクエリを実行し、その実行結果を統合して最終的な結果として採用するHybrid Searchというものがあります。

Hybrid Searchでは各クエリで算出されたスコアを統合するためのアルゴリズムとしてRRFとDBSFが選択可能です。それぞれの詳細について解説します。
Reciprocal Rank Fusion(RRF)
RRFはクエリの結果に対して逆順位スコアを割り当てるアルゴリズムです。RRFは各クエリを実行した結果の「順位」を利用するアルゴリズムで、各クエリのスコアは統合後のスコアに影響を与えません。例を見ながら考えていきましょう。

この図は右に行くほどスコアが高いということを表しています。クエリ1の赤とクエリ2の黄色を比較すると、クエリ2の黄色の方が右に位置している=スコアが高いのですが、計算後の逆順位スコアは両方とも0.33...となります。

ロジックはこの辺りです。
Distribution-Based Score Fusion(DBSF)
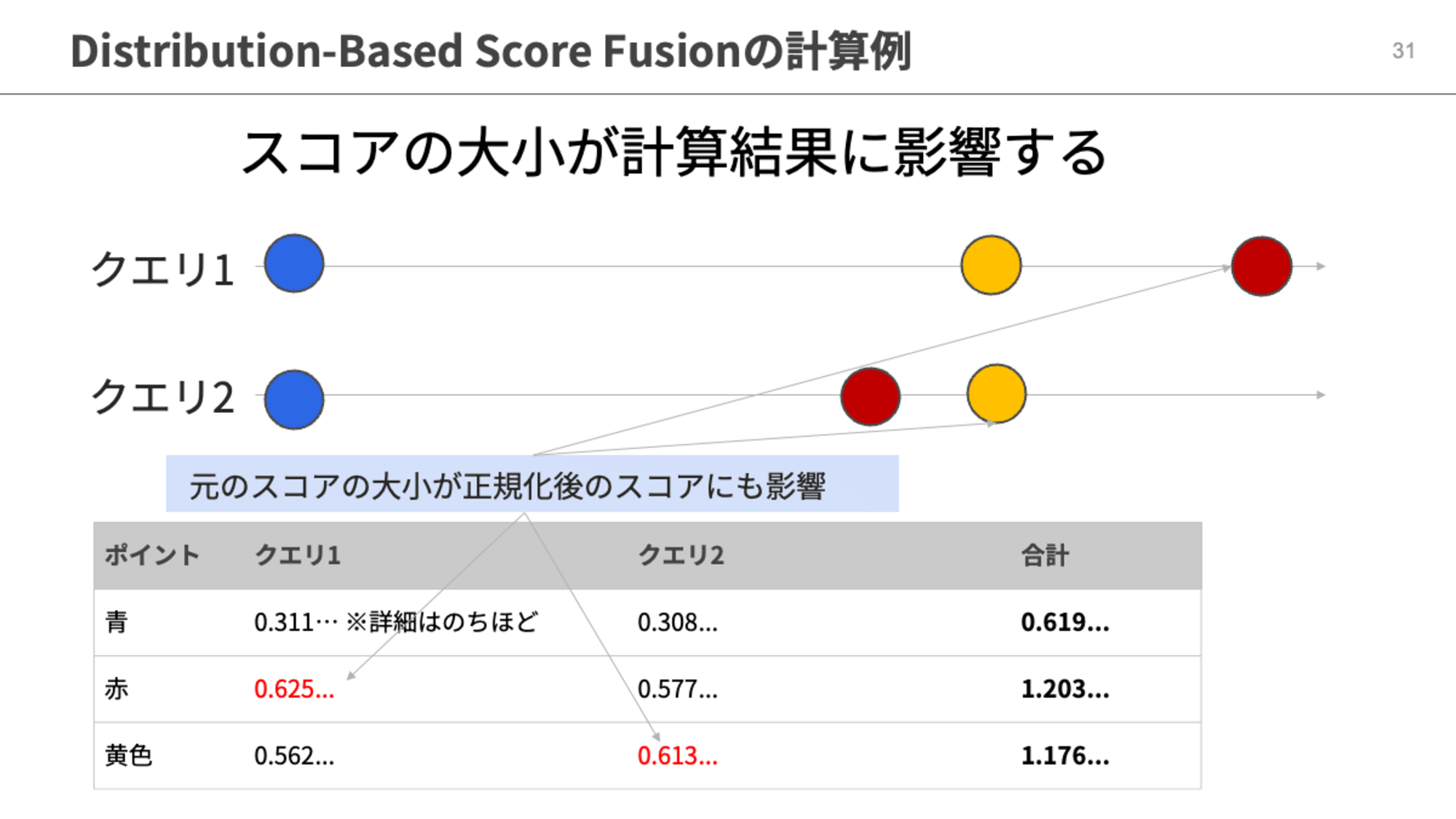
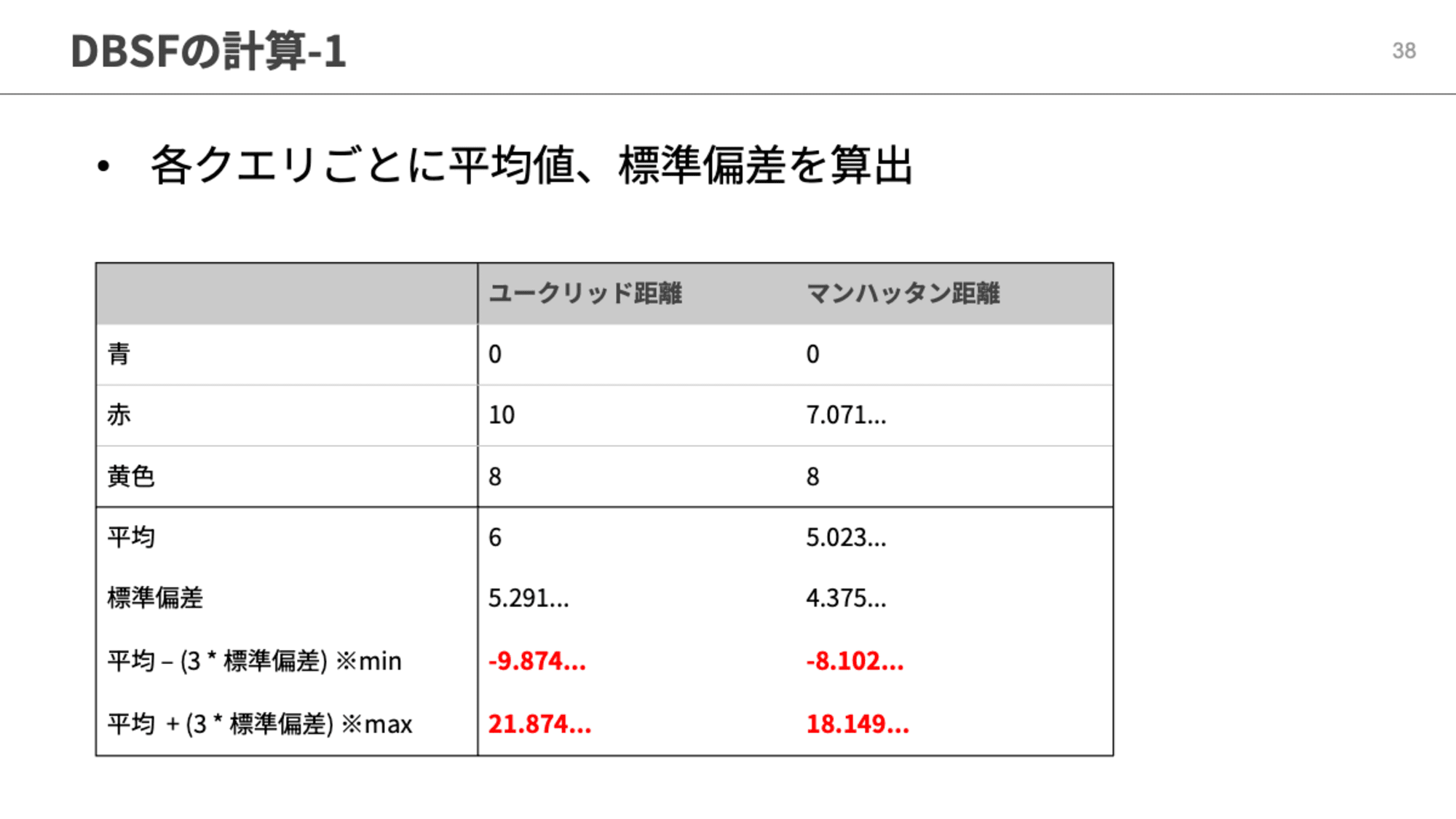
もう1つのアルゴリズムがDBSFです。こちらは各クエリの結果を正規化して融合させるアルゴリズムです。RRFとは異なり各クエリのスコアの大小が統合後のスコアにも影響を与えます。

この例だとクエリ1の赤とクエリ2の黄色は両方とも各クエリの中ではスコアが1位になっていますが、スコアの大小でいうとクエリ1の赤の方が大きくなっています。DBSFでスコアを正規化するとクエリ1の赤はスコアが0.625となり、クエリ2の黄色を正規化した0.613よりも大きなスコアとなります。
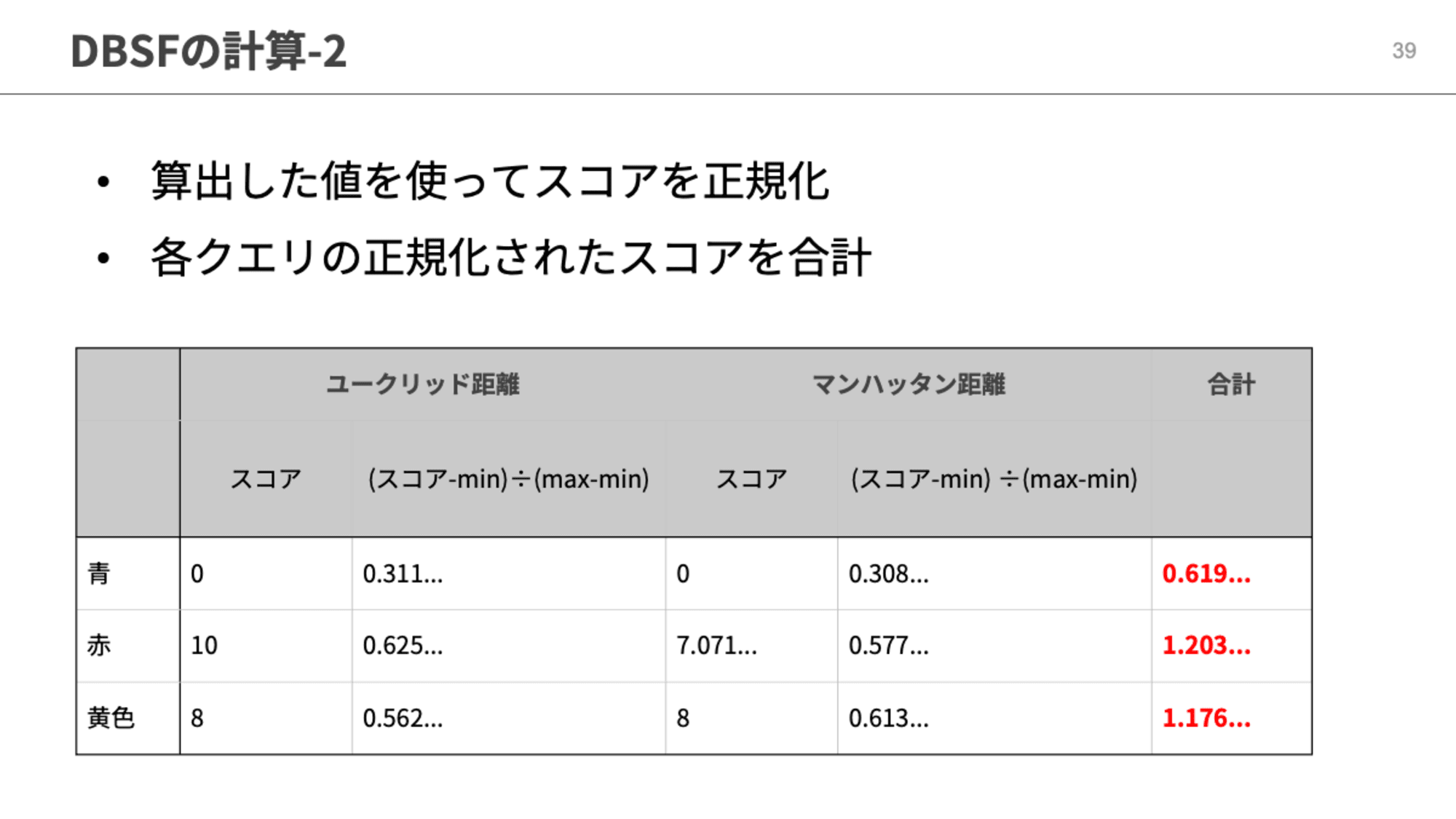
計算ロジックはこの辺りです。
Qdrantは入門にオススメ!!
ここまでベクトルデータベースに関する基礎的な概念について説明してきました。QdrantはOSSなので実際のソースコードを見ながら勉強した概念について理解を深めることができます。ぜひQdrantを触ってベクトルデータベースに入門してみてください。
登壇資料
まとめ
今回登壇駆動でベクトルデータベースやQdrantについて学んでみたのですが、QdrantがOSSで開発されているというのは学習用に非常に有用だと感じました。DBSFの計算ロジックなど色々と調べてもなかなかピンとこなかったのですが、Qdrantのソースコードを読むことで理解が深まりました。
Qdrantのソースコードを読む → EXCEL等を使って自分でスコアを計算してみる → 実際にQdrantにデータを登録&クエリして答え合わせする
という一連のプロセスを楽しみながら学ぶことができました。
ぜひ皆さんもQdrantを触ってみてください。










