
NumPyのブロードキャストを図で理解する
この記事は公開されてから1年以上経過しています。情報が古い可能性がありますので、ご注意ください。
データアナリティクス事業本部機械学習チームの中村です。
今回は、tensorflowやpytorchなどでも良く使用する配列操作やブロードキャストなどを
絵で理解していきたいと思います。
コードは簡単のため、NumPyで例示しますが考え方は他のライブラリにも応用可能です。
冒頭まとめ
- ブロードキャストが実行できる条件を列挙します。
- 多次元配列の構造をツリーで可視化して理解します。
- ブロードキャストをツリーで可視化した上で理解します。
- その後、例として画像データのような形状のものを使い、ブロードキャストの実例を示します。
- またバグになりやすいreshapeとtransposeの違いについても説明します。
ブロードキャストの実行可否条件
ブロードキャストの実行ができるためのルールは以下です。
A,Bを演算したい場合に、shapeの次元数が同じだと、1の部分を複製して演算できます。
A,Bのshapeの値がそれぞれの要素数1以外の次元では同じ要素数である必要があります。
- 例1:
A: shape=(4,3,2)とB: shape=(1,3,2)の演算は可能B: shape=(1,3,2)と同じものを4個複製し、B': shape=(4,3,2)としてから計算
- 例2:
A: shape=(4,1,2)とB: shape=(1,3,1)の演算は可能A: shape=(4,1,2)と同じものを3個複製し、A': shape=(4,3,2)としてから計算B: shape=(1,3,1)と同じものを8個複製し、B': shape=(4,3,2)としてから計算
またshapeの次元数が異なる場合でも、shapeの左側には1を自動追加することができます。
- 例3:
A: shape=(4,3,2)とB: shape=(3,2)の演算は可能B: shape=(3,2)の左に1を追加して、B': shape=(1,3,2)とする。B'と同じものを4つ複製し、B'': shape=(4,3,2)としてから計算。
- 例4:
A: shape=(4,3,2)とB: shape=(2)の演算は可能B: shape=(2)の左に1を2個追加して、B': shape=(1,1,2)とする。B'同じものを12個複製し、B'': shape=(4,3,2)としてから計算
左側と違い、shapeの右側には1を追加できません。
- 例5:
A: shape=(4,3,2)とB: shape=(4,3)の演算は不可- 理由は、右側に追加を許してしまうと、複数の解釈が可能な場合が発生するためと推測されます。
- 右側へ次元を追加したい場合は、reshapeなどを使って明示的に実行しましょう。
A,Bのshapeの値がそれぞれの要素数1以外の次元で異なると、演算はできません。
- 例6:
A: shape=(4,3,2)とB: shape=(2,3,2)の演算は不可
…ルールとしては理解できますが、いったいどのようにイメージすれば良いのでしょうか?
そもそも配列が2次元以上になると急に理解が難しくなりますよね。
そこで、今回多次元配列をツリー上で可視化することによって説明を試みてみました。
配列をツリーとして理解する
配列とは
そもそも配列とは何でしょうか?
簡単に言うなら何かの数値が集まっていて、それをひとまとまりに捉えたものと理解すればOKそうですよね。
なので基本的にこんな風に一列に並んでいるものをイメージするかと思います。

番号は要素の番号です。(数が分かりやすいように今回は1から始めてます)
せっかくなので(?)ひとまとまりということがわかるように、枝でつないでおきましょう。
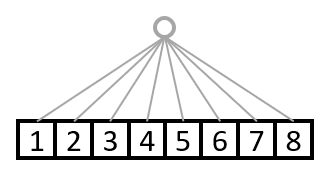
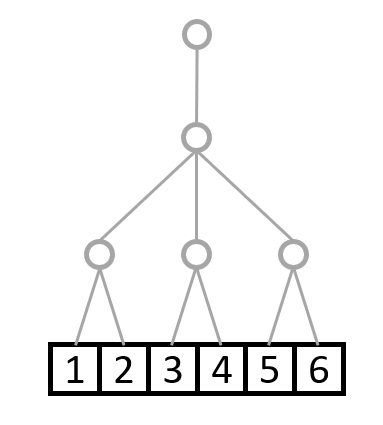
これが次元数1でshape=(8,)の配列と考えてください。
コードとしては以下のような感じで作成できます。
import numpy as np
A = np.random.randn(8)
print(A.shape)
# OUT -> (8,)
多次元配列の理解
実は多次元配列もほとんど変わりません。
さっきの枝が少し変わるだけですね。こんな感じです。
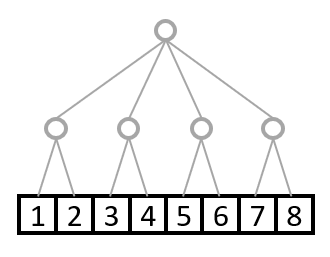
これが次元数2でshape=(4,2)の配列と考えてください。
枝の数を上から順に数えれば、shapeがわかりますね。
コードとしては以下のような感じで作成できます。
A = np.random.randn(4,2)
print(A.shape)
# OUT: (4, 2)
いかがでしょうか?次元数2だと普通行列と考えてしまうので、以下のようにイメージしがちですよね。
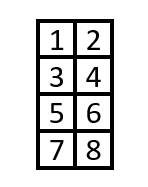
でもこのイメージだと次元数2以上の多次元配列がイメージできなくなってしまいます。
ツリーで理解すると、どんなに多次元でも拡張ができます。
序盤の例で出したshape=(4,3,2)はこんな感じになります。
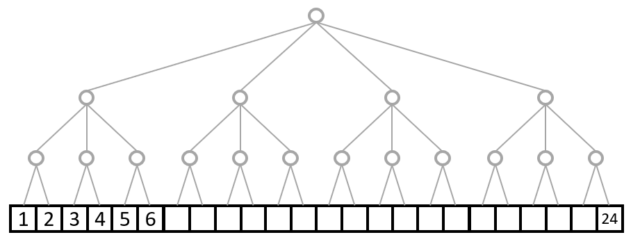
上から枝の数が4,3,2となっていて、shape=(4,3,2)に対応しています。
本来はこれらの枝数にバッチサイズや縦横の幅、チャンネル数などの意味を割り当てていくことになります。
ブロードキャストの理解
この配列をツリー構造として理解したうえで、ブロードキャストを理解してみましょう。
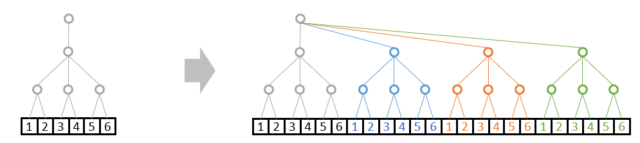
例1:A: shape=(4,3,2) と B: shape=(1,3,2)の演算は可能
A: shape=(4,3,2)は直前でお見せしたこの形と同じです。

B: shape=(1,3,2)は最上位の枝が1本になるため、このような形です。
演算時、ブロードキャストは、枝が1本の部分は相手に合わせて複製されれます。
これで先ほどのAと加算することが可能です。
コードではこのようになります。
A = np.random.randn(4,3,2)
B = np.random.randn(1,3,2)
print((A+B).shape)
# OUT: (4, 3, 2)
例2:A: shape=(4,1,2) と B: shape=(1,3,1)の演算は可能
A: shape=(4,1,2)は真ん中の枝が3つに複製されます。
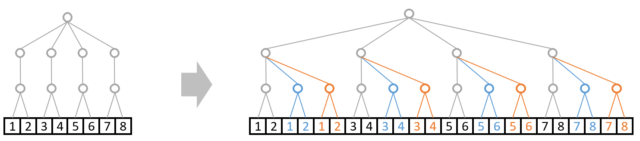
B: shape=(1,3,1)は最下層の枝と最上層の枝がそれぞれAにあわせて複製されます。
これで無事に演算できますね。
コードではこのようになります。
A = np.random.randn(4,3,2)
B = np.random.randn(1,3,1)
print((A+B).shape)
# OUT: (4, 3, 2)
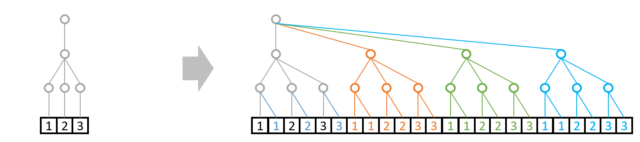
例3:A: shape=(4,3,2) と B: shape=(3,2)の演算は可能
A: shape=(4,3,2)は今まで出てきたこの形と同じです。

B: shape=(3,2)はそのままでは次元数が違いますので複製もできません。
その際追加のルールとして、以下のように上位には枝を自動で足すことが許されています。
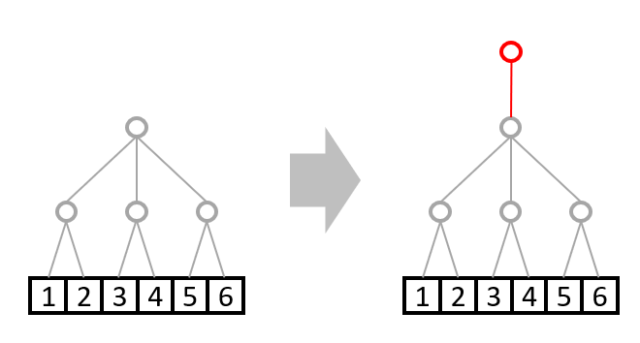
その後、例1と同様に1本の部分を複製します。

これで無事に演算できますね。
コードではこのようになります。
A = np.random.randn(4,3,2)
B = np.random.randn(3,2)
print((A+B).shape)
# OUT: (4, 3, 2)
自動で追加できるのは、上層側だけですので、下層側に追加したい場合はreshapeで明示的に変形します。
A = np.random.randn(4,3,2)
B = np.random.randn(4,3).reshape(4,3,1)
print((A+B).shape)
# OUT: (4, 3, 2)
ブロードキャストの実用例
例がないとイメージがわかない部分もありますので、画像データをイメージしてみます。
画像データのshapeはshape=(バッチ数, 高さ, 幅, チャネル数)などで与えられることが多いですね。
そういったデータを定義しましょう。
A = np.random.randn(100, 224, 224, 3)
print(A.shape)
# OUT: (100, 224, 224, 3)
このAはあるバッチ分のデータセットとみなせます。
バッチ内の各位置で全チャンネルの平均を得たい場合どのようにするでしょうか。
以下のように、集約したいaxisを指定してnp.meanをすれば計算できます。
A_mean = np.mean(A,axis=(0,3))
print(A_mean.shape)
# OUT: (224, 224)
これで各位置毎の平均値が取得できています。
axis=(0,3)はツリーでいうところの0が最上層、3が最下層を指定しています。
指定した層について平均を計算するという意味となりますので、残りの間の2つの枝(224,224)が残ります。
これを元のAから差し引く場合、以下のようにします。
B = A - A_mean.reshape(224,224,1)
print(B.shape)
# OUT: (100, 224, 224, 3)
A_meanはshape=(224,224)なので、上位と下位に枝を足さねばなりません。
上位には自動追加が使えますので、下位に明示的にreshapeすることで枝を足しています。
一連の処理は、np.meanにあるkeepdims引数を指定することで、shapeを維持したまま分かりやすくすることもできます。
A_mean = np.mean(A, axis=(0,3), keepdims=True)
print(A_mean.shape)
# OUT: (1, 224, 224, 1)
これだとそのまま演算してもエラーにはなりません。
B = A - A_mean
print(B.shape)
# OUT: (100, 224, 224, 3)
reshapeってところで何ですか?
reshapeはここまで見てきたように、枝を付け替えるだけの作業と理解すればOKです。
以下のreshapeを考えます。
A = np.random.randn(2,4)
A_reshaped = A.reshape(4,2)
このreshapeは以下の図のような枝の付け替えと同じです。
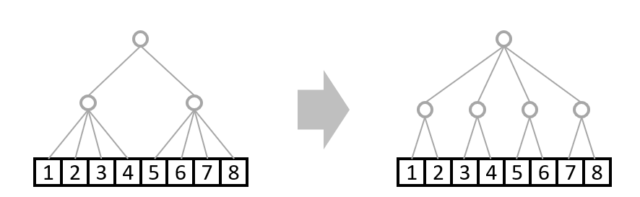
ただしこういったreshapeは意図通りでない場合が多いです。
例えば元のツリーにおける上層の枝がバッチ数を、下層の枝が入力ベクトルの要素番号であるとした場合、
reshape後の枝は、上層が各バッチを要素を一つずつ飛ばしながら読む形となり、論理的な意味を成していません。
reshape処理自体はエラーになりませんので、実際こういったケースでバグとなってしまうことも多いです。
reshapeとtransposeの違い
これを解決するためには、transposeを用いる必要があります
transposeはそもそものデータの並び順を変更し、層における枝の意味合いを入れ替えることが可能です。
A = np.random.randn(2,4)
A_transpose = A.transpose(1,0)
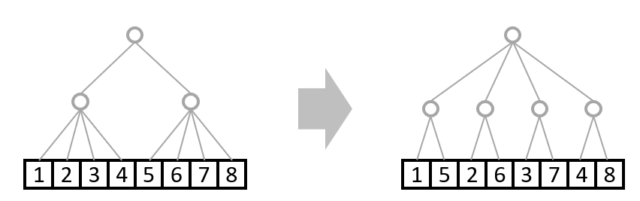
まとめ
いかがでしたでしょうか?後半のnp.transposeはなれないと難しい部分もありますが、
とりあえず多次元配列をツリー構造ととらえることで、多次元配列は所詮一列に並んでいて、
アクセスするための枝がいろいろあるだけという理解をすれば、抵抗感が薄まるのかなと考えています。
これをヒントに色々遊んで頂き、NumPy配列の扱いに慣れていただけたら幸いです。









