[Python][Scipy] 様々な距離でボロノイ図を作成してみた

はじめに

K-means法やk近傍法等のクラスタリングで用いられる距離については、クラスタリングする対象によっては距離として私達が普段馴染んでいるユークリッド距離以外の距離を用いるとうまくいくケースがあります。（Mahout イン・アクション）

私達が普段馴染んでいるユークリッド距離と書きましたが、このユークリッド距離は2つのベクトル \( \boldsymbol{x}, \boldsymbol{y} \) が与えられたとき、次のように定義されます。

[latex] d_{\text{euclid}}(\boldsymbol{x}, \boldsymbol{y}) = \sqrt{\sum^n_{i = 1} (x_i - y_i)^2} [/latex]

この距離という概念は数学的には類似度を測る尺度として抽象化され、2つのベクトルを引数としてとり実数を返却する関数 \( d\) は下記の距離の公理を満たせば距離としてみなすことができます。

[latex] d(\boldsymbol{x}, \boldsymbol{y}) \geq 0 [/latex]

[latex] d(\boldsymbol{x}, \boldsymbol{y}) = 0 \ \text{となるのは次の場合のみ→} \ \boldsymbol{x} = \boldsymbol{y} [/latex]

[latex] d(\boldsymbol{x}, \boldsymbol{y}) = d(\boldsymbol{y}, \boldsymbol{x}) [/latex]

[latex] d(\boldsymbol{x}, \boldsymbol{z}) \leq d(\boldsymbol{x}, \boldsymbol{y}) + d(\boldsymbol{y}, \boldsymbol{z}) [/latex]

このような今回は性質をみたすような距離として、Scipyにある様々な距離関数を用いてクラスタリングでよく用いられるボロノイ図を図示してみました。

ボロノイ図

ボロノイ図は、クラスタを代表するベクトル（母点）が複数定義されている時に、空間上の任意の点がどのクラスタに属するかを調べるために用います。

(ボロノイ図 - Wikipediaより引用）

この図は距離の取り方によって変化するため、母点を固定した上で距離をいろいろ変えてみて、クラスタリングのための距離としてどのようなものを採用したらいいか、図から判定したいです。

サンプルコード

ボロノイ図を各距離に合わせて出力するコードはGithubに上がっています。

環境

• python: anaconda-4.0.0

ソースコードの概要

In [1]:

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
%matplotlib inline

def label_cluster_num(means, mesh_points, metrics):
    def label(point):
        cluster_label = np.argmin(map(lambda mean: metrics(mean, point), means))
        return point, cluster_label
    return map(label, mesh_points)

• l6 : 母点のリストmeans、xy平面上のメッシュポイントのリストmesh_points、距離関数metricsを指定してメッシュポイントにラベル付けを行う関数です。
• l7 : 関数内部でメッシュポイントへのラベル付けを行う関数です。
• l8 : 単一のメッシュポイントが各母点からどのくらい離れているかを計算し、最小値をとるようなインデックスをcluster_labelに格納します。
• l9 : mesh_pointsをマッピングすることで各メッシュ点へのラベル付を行います。

In [2]:

c_means = np.array([[1, 2], [-3, 4], [-5, -6], [7, -8]])
xs = np.linspace(-10, 10, 100)
ys = np.linspace(-10, 10, 100)
xx, yy = np.meshgrid(xs, ys)
mesh_points = np.c_[xx.ravel(), yy.ravel()]

• l1 : 母点のサンプルを c_means に格納します。
• l2-5 : 以前の記事でも紹介していますが、この辺りの処理は (【Python】ふたつの配列からすべての組み合わせを評価 - keisukeのブログ)に詳しいです。やっていることとしては、-10~10までの区間のxy平面上に等間隔に並べられた10000個のメッシュ点を作成し、そのベクトルを配列としてmesh_pointsに格納しています。

In [3]:

def show_volonoi_with_metrics(metrics):
    labeled_mesh_points = label_cluster_num(c_means, mesh_points, metrics=metrics)
    plt.figure()
    fig, ax = plt.subplots()

    ax.set_aspect('equal')
    ax.grid(True, which='both')
    ax.axhline(y=0, color='k')
    ax.axvline(x=0, color='k')
    ax.set_xlim([-10, 10])
    ax.set_ylim([-10, 10])

    for i in range(0, len(c_means)):
        cluster_points = map(lambda (p, label): p, filter(lambda (p, label): label == i, labeled_mesh_points))
        xs = map(lambda p: p[0], cluster_points)
        ys = map(lambda p: p[1], cluster_points)
        ax.scatter(xs, ys, color=cm.prism(i / float(len(c_means))), marker='.')

    ax.scatter(map(lambda p: p[0], c_means), map(lambda p: p[1], c_means), color="g", marker='o')

    plt.show()

• l1 : 距離を指定してボロノイ図を出力する関数を定義しています。
• l2 : メッシュ点に対してラベル付を実施し、labeled_mesh_points に格納します。
• l3 : subplots 関数は matplotlib.figure.Figure オブジェクトと matplotlib.axes.Axes オブジェクトをタプルとして返却します。Figureオブジェクトは図に描画する要素のトップレベルのコンテナ、Axesオブジェクトは描画する図形等を保持するオブジェクトで、座標系も管理します。
• l6-11 : 座標や背景のグリッド線等の各種設定を行います。
• l13 : ラベル毎に異なる色で各メッシュ点にプロットしていきます。
• l14 : プロットすべきメッシュ点を抽出します。
• l17 : 各クラスタ毎のメッシュ点をプロットします。色はmatplotlib.cmモジュールに定義されたカラーパレットで取得しています。
• l19 : 各母点を最後にプロットします。

各距離に対応したボロノイ図

上記関数を用いたプロットの為のコードと出力したボロノイ図は次の通りです。出力の前に以下のインポート文を走らせています

import scipy.spatial.distance as dist

ユークリッド距離

[latex] d_{\text{euclid}}(\boldsymbol{x}, \boldsymbol{y}) = \sqrt{\sum^n_{i = 1} (x_i - y_i)^2} [/latex]

show_volonoi_with_metrics(dist.euclidean)

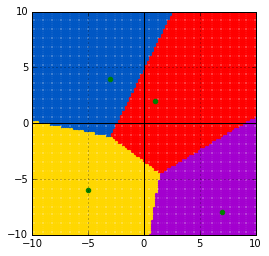
コサイン距離

[latex] d_{\text{cosine}}(\boldsymbol{x}, \boldsymbol{y}) = \frac{\sum^n_{i = 1} x_i y_i}{\sqrt{ ( \sum^n_{i = 1} x_i ^ 2) ( \sum^n_{i = 1} y_i ^ 2) }} [/latex]

show_volonoi_with_metrics(dist.cosine)

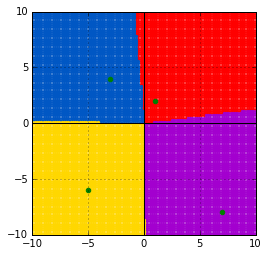
マンハッタン距離

[latex] d_{\text{manhattan}}(\boldsymbol{x}, \boldsymbol{y}) = \sum^n_{i = 1} | x_i - y_i | [/latex]

show_volonoi_with_metrics(dist.cityblock)

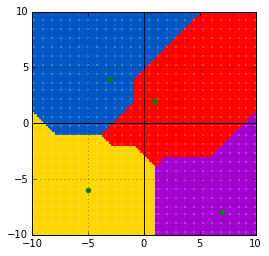
チェビシェフ距離

[latex] d_{\text{chebyshev}}(\boldsymbol{x}, \boldsymbol{y}) = \max_i | x_i - y_i | [/latex]

show_volonoi_with_metrics(dist.chebyshev)

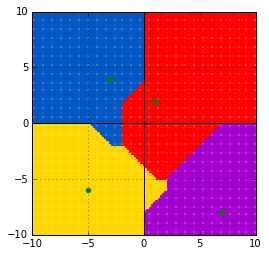
キャンベラ距離

[latex] d_{\text{canberra}}(\boldsymbol{x}, \boldsymbol{y}) = \sum^n_{i = 1} \frac{ | x_i - y_i | }{ |x_i| + |y_i| } [/latex]

show_volonoi_with_metrics(dist.canberra)

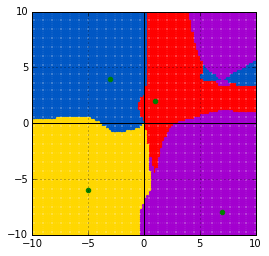
まとめ

この記事を書こうと思ったきっかけとしては社内勉強会で通読中のITエンジニアのための機械学習理論入門のクラスタリングの章を読んでいて、クラスタリングの境界がデータにフィットしているとはどういうことかというトピックが出た際に、k-means法でもクラスタリングの境界が必ずしも直線状にならないケースがあることを説明する必要に迫られて、距離毎にこのような境界が図示できるというイメージを自分のなかで付けたかったからです。 上記スクリプトは母点、距離関数を自由に変えられますので、クラスタリングの際に距離を変更することを検討したい時にぜひご活用ください！

参考

• Sean他 Mahout イン・アクション - オライリー・ジャパン
• 平井 有三 はじめてのパターン認識 - 森北出版 2012