
数学が苦手なのでCognitoでも使用するSRPの仕組みをなんとなくわかった風に図解する
はじめに
こんにちは、コンサルティング部のぐっさんです。
私は数学が本当〜〜〜〜に苦手です。
本記事では、SRP(Secure Remote Password) という数学の計算をがっつり用いたパスワード認証の仕組みを、苦手すぎる自分の見解を交えてカジュアルにご紹介します。
SRP とは?
一言でいうと、「パスワードを送らずに、パスワードを知っていることを証明する」 仕組み(プロトコル)です。
Amazon Cognito のカスタム認証でも使われており、pycognito ライブラリなどが内部で SRP を処理しています。
一応、RFC2945も一通り目を通しました。
公式の算出式を確認されたい方は、こちらをどうぞ。なお私には難しすぎました。。。
従来の認証の問題点
まず、一般的な従来のパスワード認証の流れを見てみましょう。
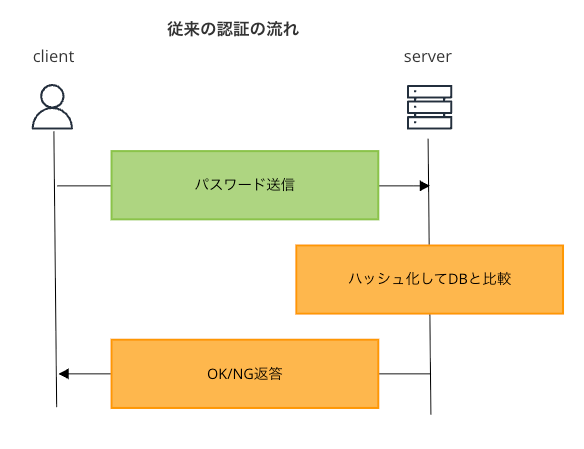
問題点
| 問題 | 説明 |
|---|---|
| 盗聴リスク | パスワードがネットワークを流れる |
| サーバー漏洩リスク | パスワード(のハッシュ)がDBに保存されている |
| フィッシング | 偽サイトにパスワードを入力したら盗まれる |
この通り、セキュリティ面ではあまり強固な認証方法とは言い難いですね。
SRP の基本的な思想
核心となる考え方
- イメージ
「パスワードを教えて」ではなく
「パスワードを知っていないと解けない問題を出すから解いてね」
正解できた = パスワードを知っている証拠となる、というわけです。
認証のイメージを身近な例に落とし込むと・・・
例えば仮に、座標的なデータを想像します。
「秘密のスタート地点を相手に明かさずに、同じ待ち合わせ場所に到着できることを証明する」仕組みを考えましょう。
先に全体イメージ:
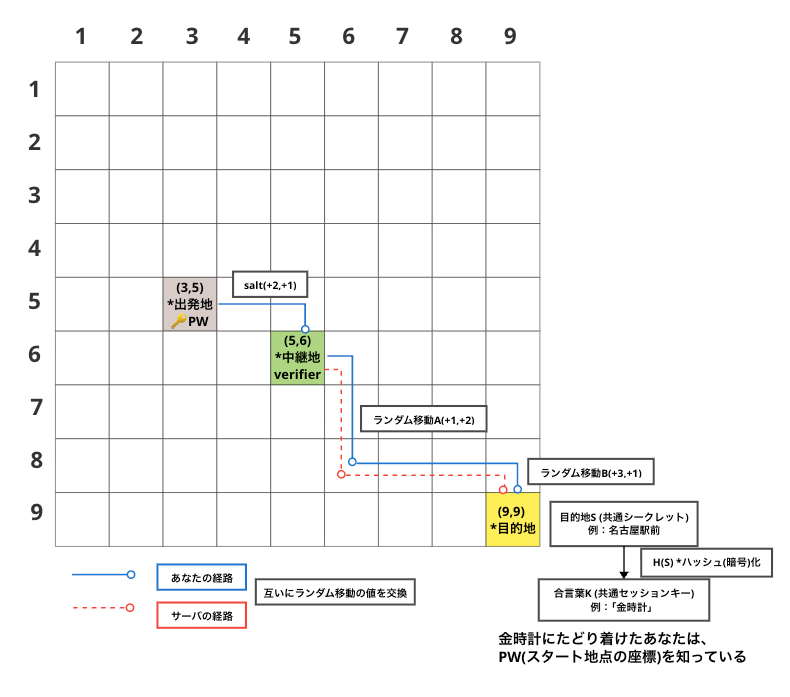
登場人物と用語
| あなた(クライアント) | 友人(サーバー) | |
|---|---|---|
| 自宅/スタート地点(password) | ✓ 知っている | ✗ 知らない |
| 移動距離α(salt) | ✓ 知っている | ✓ 知っている |
| 中継地点(verifier) | 計算できる | 保存済み |
| 例え | 技術用語 | 説明 |
|---|---|---|
| 自宅/スタート地点の座標 | password | あなただけが知っている秘密 |
| 移動距離α | salt | 登録時に決めるランダムな移動距離 |
| 中継地 | verifier | 家から移動距離α分進んだ地点(サーバーが保存) |
| 移動距離A・B | A, B | 毎回ランダムに決める移動距離 |
| 名古屋駅 | S(共通シークレット) | 両者が到着する待ち合わせ場所 |
| 金時計 | K(セッションキー) | S からハッシュ(暗号化)計算を行い導出した合言葉 |
【登録時】待ち合わせのルールを決める
最初に一度だけ、中継地を友人に教えます。
あなたの情報:
- 自宅/スタート地点: (3, 5) ← パスワード(秘密!)
- 移動距離α: (+2, +1) ← salt(ランダムに決めてハッシュ化)
計算:
自宅/スタート地点(3,5) → 移動距離α(+2,+1) → 📍中継地(5,6)
友人に渡す情報:
| 情報 | 渡す? |
|---|---|
| 移動距離α (+2, +1) | ✓ 渡す |
| 中継地点 (5, 6) | ✓ 渡す |
| 家の場所 (3, 5) | ✗ 渡さない! |
【認証時】待ち合わせ場所で会う
毎回ランダムな移動距離を決めて、同じ場所に到着できるか確認します。
今日の移動距離(ランダムに決める):
| 誰が決める | ランダムな移動距離 |
|---|---|
| あなた | A: (+1, +2) |
| 友人 | B: (+3, +1) |
あなたのルート
自宅/スタート地点(3,5) → 移動距離α → 📍中継地(5,6) → ランダム移動距離A → ランダム移動距離B → 名古屋駅(9,9)
| ステップ | 座標 or 移動量 |
|---|---|
| 自宅/スタート地点 | (3, 5) |
| 移動距離α | +2, +1 |
| 中継地 | (5, 6) |
| 移動距離A | +1, +2 |
| 移動距離B | +3, +1 |
| 名古屋駅(到着) | (9, 9) |
友人のルート
📍中継地(5,6) → ランダム移動距離A → ランダム移動距離B → 名古屋駅(9,9)
| ステップ | 座標 or 移動量 |
|---|---|
| 中継地 | (5, 6) ← 打ち合わせ済み |
| 移動距離A | +1, +2 |
| 移動距離B | +3, +1 |
| 名古屋駅(到着!) | (9, 9) |
※ 家の場所は知らないが、同じ場所に到着できる
名古屋駅で合言葉を交わす
S → K の導出:
| ステップ | 内容 |
|---|---|
| S(名古屋駅) | (9, 9) |
| ↓ ハッシュ化 | H(S) |
| K(合言葉) | 「金時計」 |
合言葉の確認:
| 方向 | メッセージ |
|---|---|
| あなた → 友人 | M1「金時計の前にいます」 |
| 友人 → あなた | M2「私も金時計の前です」 |
→ 合言葉が一致 = お互いが本人だと確認
※これは本当に簡単な例えになりますので、厳密にはもっと複雑な計算が走っています。
改めて、イメージです!
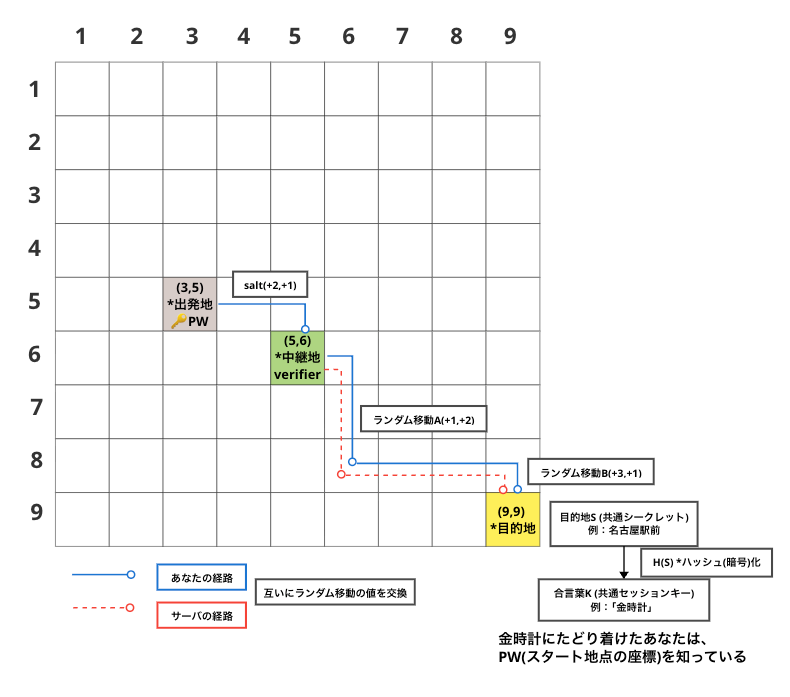
なぜこれで証明になる?
正しい家からでないと到着できない
| ルート | 結果 | |
|---|---|---|
| 正規ユーザー | 家(3,5) → 移動α → 移動A → 移動B | 名古屋駅(9,9) ✓ |
| 攻撃者 | ??? → 移動α → 移動A → 移動B | (?,?) ✗ |
→ 正しい家の座標(パスワード)を知らないと、名古屋駅には到着できない
攻撃者がなりすまそうとすると:
攻撃者: (?, ?) + (2,1) + (1,2) + (3,1) = (9, 9) になる ? を探す
でも...
・中継地点 (5, 6) は盗聴できる
・移動量 (+2, +1) も盗聴できる
・(5, 6) - (2, 1) = (3, 5) で計算できてしまいそう...?に思いますよね。それは私も思いました。
ここが実際のSRPのポイント
上の例では単純な足し算なので逆算できてしまいますが、
実際の SRPの計算 では「一方向関数」なるものを使います。(3, 5) + (2, 1) → 特殊な変換 → (?, ?) ↑ この変換は逆算できません (離散対数問題)よって中継地点を見ても、元のスタート地点は数学的に求められません。
技術用語との対応
| 待ち合わせの例え | 技術用語 | 値の例 |
|---|---|---|
| 自宅の座標 | password | (3, 5) |
| 移動距離α | salt | (+2, +1) |
| 中継地点 | verifier | (5, 6) |
| 移動距離A | A(クライアント公開値) | (+1, +2) |
| 移動距離B | B(サーバー公開値) | (+3, +1) |
| 名古屋駅 | S(共通シークレット) | (9, 9) |
| 金時計 | K(セッションキー) | H(S) |
| 「金時計の前にいます」 | M1 | Kを知っている証明 |
| 「私も金時計の前です」 | M2 | サーバーもKを知っている証明 |
認証フローを図解
登録時(一度だけ)
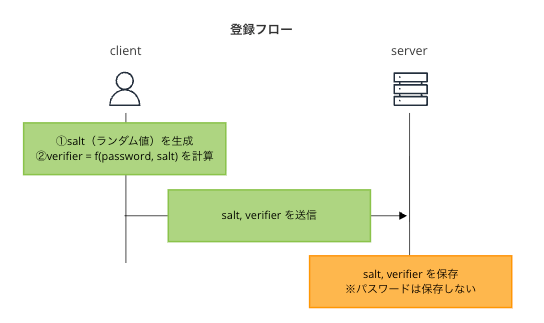
ログイン時
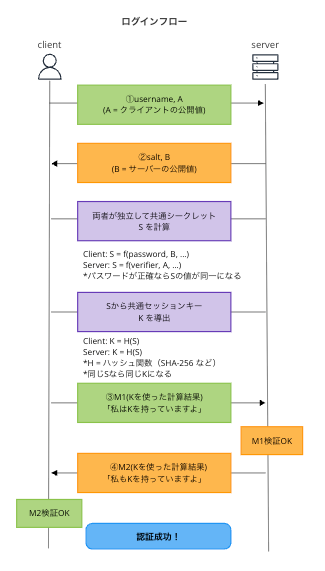
なぜ安全なのか
1. パスワードがネットワークを流れない
【従来】スタート地点を送信 → 盗聴されたら終わり
【SRP】 移動A, M1 を送信 → スタート地点は逆算できない
2. サーバーが攻撃されても安全
【従来】スタート地点のハッシュが漏洩 → 総当たり攻撃可能
【SRP】 中継地点が漏洩しても:
→ スタート地点は逆算できない(一方向関数)
→ 中継地点だけではログインできない(計算式が異なる)
3. リプレイ攻撃に強い
移動A, 移動B は毎回ランダムに変わる
→ 待ち合わせ場所も毎回変わる
→ 過去の通信を再利用できない
4. 相互認証
M2 により、サーバーも正しい中継地点を持っていることを確認
→ 偽サーバー(フィッシング)対策
まとめ
SRP(Secure Remote Password)は、パスワードを送らずに認証できるプロトコルです。
本格的に中身を計算をすると複雑な(私には到底理解不能な)計算になりますが、なんとなく・・・のイメージでも掴めたら嬉しいです。
| 特徴 | 説明 |
|---|---|
| パスワードを送らない | スタート地点はネットワークを流れない |
| サーバーにパスワードを保存しない | 中継地点のみ保存。漏洩しても安全 |
| 相互認証 | クライアントもサーバーを検証できる |
| リプレイ攻撃耐性 | 毎回ランダムな移動を使うので再利用不可 |
「秘密のスタート地点を明かさずに、同じ待ち合わせ場所に到着できることで本物と証明する」
このイメージを持っておくと、SRP の本質を理解する足掛けになるかなと思います。
以上、お読みいただきありがとうございました!








