座標変換について調べてみた

山本紘暉

2020.07.09

この記事は公開されてから1年以上経過しています。情報が古い可能性がありますので、ご注意ください。

カフェチームの山本です。

現在、カフェチームでは、機械学習を用いて、画像内に映っている人物の骨格や手を検出することで、どの商品を取り出したかを判定する方法を検討しています。

今回は、その前段階として、座標変換について調べた内容についてまとめました。

本記事と異なる定義を用いている説明もありますので、混乱されないようご注意ください。正直なところ、解説する方ごとに定義が異なっていたり、目的どおりの計算が載ってなかったりと、かなり難しかったです。備忘録としてまとめていますが、間違っているところがあったら、コメント等でお教えいただけると大変助かります！

お詫び

本ページの数式が正しく表示されていません。現在、修正中です。数式まで見たい方はこちらのページをご覧ください。

座標変換について調べてみた

０．用語の定義

説明にあたって、利用する用語を定義しておきます。

基礎用語

座標系：原点と軸のセット。
基底（ベクトル）：座標系の各軸の方向を向き、長さ１のベクトル。またはそのセット。
位置：空間（平面）中の位置。
座標：空間中の位置を、座標系における基底ベクトルの線形和で表現したもの。空間中の同じ位置であっても、座標系によって座標が変わります。
回転：座標系の軸における回転。右手系の場合、軸が正となる方向から原点を向いて、左回り（反時計周り）が正です。
右手（直交座標）系：下図のように、右方向をx軸、下方向をy軸・奥方向をz軸とする座標系。x軸・y軸・z軸の相対関係が右手の親指・人差し指・中指の向きのようになっています。

左：左手系　右：右手系

画像は、https://ja.wikipedia.org/wiki/右手系　より

変換する座標系

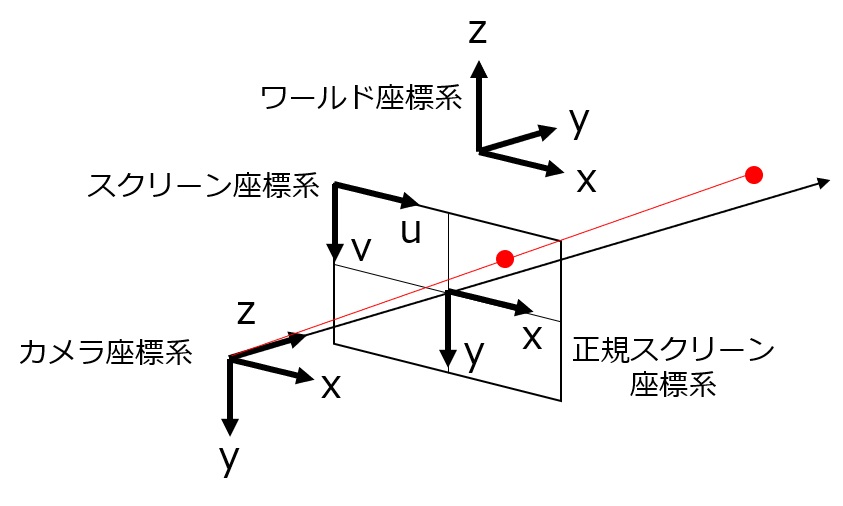
ワールド座標系：基準となる座標系。今回は右手系とします。
カメラ座標系（ビュー座標系）：実際の空間に存在するカメラの位置を原点として、注視する方向にz軸、z軸に垂直な面における右方向をx軸、下方向をy軸とした座標系。
正規スクリーン座標系：カメラ座標系からみた位置を、z=1の平面に透視投影した際の、平面における座標。z軸との交点を原点として、x軸とy軸が元のカメラ座標系と同じ方向。
スクリーン座標系：正規スクリーン座標系を、カメラで撮影した場合の座標に変換したもの。スクリーンの大きさの1/2分、原点が左上のずれている。画面右方向をu軸（x軸）、下方向をv軸（y軸）とする。また、カメラ座標系のz軸を、スクリーン座標系のz軸とする。u軸（x軸）とv軸（y軸）の単位はピクセル数、z軸の単位はワールド座標と同じです。

１．基本

並進（平行移動）

ある位置pを、x軸方向にtx、y軸方向にtyだけ並行移動した後の位置p'は、以下のように表すことができます。

[latex]\vec{t} = \left( \begin{matrix} t_x \\ t_y \end{matrix} \right)[/latex]

[latex]\vec{p'}=\vec{p}+\vec{t}[/latex]

回転行列

2次元の場合

ある位置pを、原点を中心にθだけ回転した後の位置p'は、以下のように表すことができます。

[latex]R(\theta)=\left( \begin{matrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{matrix} \right)[/latex]

[latex]\vec{p'}=R(\theta)\vec{p}[/latex]

3次元の場合

ある位置pを、x軸を中心にθ、y軸を中心にφ、z軸を中心にψ、順に回転した後の点p'は、以下のように表すことができます。

[latex]R_x(\theta) = \left( \begin{matrix} 1 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta \\ 0 & \sin\theta & \cos\theta \end{matrix} \right)[/latex]

[latex]R_y(\phi) = \left( \begin{matrix} \cos\phi & 0 & \sin\phi \\ 0 & 1 & 0 \\ -\sin\phi & 0 & \cos\phi \end{matrix} \right)[/latex]

[latex]R_z(\psi) = \left( \begin{matrix} \cos\psi & -\sin\psi & 0\\ \sin\psi & \cos\psi & 0 \\ 0 & 0 & 1 \end{matrix} \right)[/latex]

[latex]\begin{matrix} R_{x,y,z}(\theta,\phi,\psi) &=& R_z(\psi) \ R_y(\phi) \ R_x(\theta) \end{matrix}[/latex]

[latex]\vec{p'} = R_{x,y,z}(\theta,\phi,\psi) \ \vec{p}[/latex]

基底変換

元となる座標系における基底ベクトルex・eyを、各軸を原点を中心にθだけ回転した座標系における基底ベクトルex'・ey'に変換する場合、以下のように計算できます。ex, eyを横に並べ、右からR(θ)をかけます。

[latex]\vec{e_x} = \left( \begin{matrix} 1 \\ 0 \end{matrix} \right), \ \vec{e_y} = \left( \begin{matrix} 0 \\ 1 \end{matrix} \right)[/latex]

[latex]\left\{ \begin{matrix} \vec{e_x'} &=& \cos\theta \ \vec{e_x} + \sin\theta \ \vec{e_y} \\ \vec{e_y'} &=& -\sin\theta \ \vec{e_x} + \cos\theta \ \vec{e_y} \end{matrix} \right.[/latex]

[latex]\Leftrightarrow \left( \begin{matrix} \vec{e_x'}, \vec{e_y'} \end{matrix} \right) = \left( \begin{matrix} \vec{e_x}, \vec{e_y} \end{matrix} \right) \left( \begin{matrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{matrix} \right) = \left( \begin{matrix} \vec{e_x} , \vec{e_y} \end{matrix} \right) R(\theta)[/latex]

座標変換

ある座標系において(x, y)で表される位置pを、各軸を原点を中心にθだけ回転し、tだけ並行移動した座標系における表記(x', y')に変換する場合、以下のように計算できます。

まず、元の座標系でpを表すと、以下のようになります。

[latex]\vec{p} = \left( \begin{matrix} \vec{e_x} , \vec{e_y} \end{matrix} \right) \left( \begin{matrix} x \\ y \end{matrix} \right)[/latex]

また、変換した座標系を用いて表すと以下のようになります。

[latex]\begin{matrix} \vec{p} &=& \left( \begin{matrix} \vec{e_x'} , \vec{e_y'} \end{matrix} \right) \left( \begin{matrix} x' \\ y' \end{matrix} \right) + \vec{t} \\ &=& \left( \begin{matrix} \vec{e_x} , \vec{e_y} \end{matrix} \right) R(\theta) \left( \begin{matrix} x' \\ y' \end{matrix} \right) + \left( \begin{matrix} \vec{e_x} , \vec{e_y} \end{matrix} \right) \left( \begin{matrix} t_x \\ t_y \end{matrix} \right) \\ &=& \left( \begin{matrix} \vec{e_x} , \vec{e_y} \end{matrix} \right) \left( R(\theta) \left( \begin{matrix} x' \\ y' \end{matrix} \right) + \left( \begin{matrix} t_x \\ t_y \end{matrix} \right) \right) \end{matrix}[/latex]

２つの式は同じ位置を表してます。

[latex]\left( \begin{matrix} \vec{e_x} , \vec{e_y} \end{matrix} \right) \left( \begin{matrix} x \\ y \end{matrix} \right) = \left( \begin{matrix} \vec{e_x} , \vec{e_y} \end{matrix} \right) \left( R(\theta) \left( \begin{matrix} x' \\ y' \end{matrix} \right) + \left( \begin{matrix} t_x \\ t_y \end{matrix} \right) \right)[/latex]

式変形していきます。(ex, ey)が両辺で共通しているので、

[latex]\left( \begin{matrix} x \\ y \end{matrix} \right) = R(\theta) \left( \begin{matrix} x' \\ y' \end{matrix} \right) + \left( \begin{matrix} t_x \\ t_y \end{matrix} \right)[/latex]

[latex]\Leftrightarrow\left( \begin{matrix} x \\ y \end{matrix} \right) - \left( \begin{matrix} t_x \\ t_y \end{matrix} \right) = R(\theta) \left( \begin{matrix} x' \\ y' \end{matrix} \right)[/latex]

[latex]\Leftrightarrow R^{-1}(\theta) \left( \left( \begin{matrix} x \\ y \end{matrix} \right) - \left( \begin{matrix} t_x \\ t_y \end{matrix} \right) \right) = \left( \begin{matrix} x' \\ y' \end{matrix} \right)[/latex]

[latex]\Leftrightarrow \left( \begin{matrix} x' \\ y' \end{matrix} \right) = R^{-1}(\theta) \left( \left( \begin{matrix} x \\ y \end{matrix} \right) - \left( \begin{matrix} t_x \\ t_y \end{matrix} \right) \right)[/latex]

式変形の結果から、変換後の座標系における座標は、元の座標から平行移動分を引いて、回転行列の逆行列をかければことがわかります。

変換例

例えば、原点が(10, 5)にあり各軸がワールド座標系よりも30°回転した方向に向いている座標系において、ワールド座標の(20, 16)に対応する座標は以下のようになります。

[latex]\begin{matrix} R^{-1}(\theta) \left( \left( \begin{matrix} x \\ y \end{matrix} \right) - \left( \begin{matrix} t_x \\ t_y \end{matrix} \right) \right) &=& \left( \begin{matrix} \cos30 & -\sin30 \\ \sin30 & \cos30 \end{matrix} \right)^{-1} \left( \left( \begin{matrix} 20 \\ 16 \end{matrix} \right) - \left( \begin{matrix} 10 \\ 5 \end{matrix} \right) \right) \\ &=& \left( \begin{matrix} \sqrt{3}/2 & -1/2 \\ 1/2 & \sqrt{3}/2 \end{matrix} \right)^{-1} \left( \begin{matrix} 10 \\ 11 \end{matrix} \right) \\ &=& \left( \begin{matrix} \sqrt{3}/2 & 1/2 \\ -1/2 & \sqrt{3}/2 \end{matrix} \right) \left( \begin{matrix} 10 \\ 11 \end{matrix} \right) \\ &=& \left( \begin{matrix} \frac{10\sqrt{3}+11}{2} \\ \frac{-10+11\sqrt{3}}{2} \end{matrix} \right) \end{matrix}[/latex]

2次元平面の場合を書きましたが、3次元空間でも同様に、平行移動分を引いて、回転行列の逆行列をかけることで、変換後の座標を求めることができます。

透視変換

空間に位置する点p=(x, y, z)を原点z軸方向に見たとき、z=1の平面におけるどの座標(x’, y')に当たるかを計算します。x軸とy軸の方向は、もとの座標系と同じです。（これは、次のスクリーン変換のための前準備です）

相似の関係があるため、以下の関係が成り立ちます。

[latex]\left( \begin{matrix} x' \\ y' \end{matrix} \right) = \left( \begin{matrix} x/z \\ y/z \end{matrix} \right)[/latex]

スクリーン変換

透視投影した後の平面内での座標(x, y)が、カメラで撮影したときに撮影した映像上のどの座標(u, v)になるかには、以下の関係があります。カメラは座標系の原点にあり、x軸と同じ方向にu軸、y軸と同じ方向にv軸があるものとします。また、今回は、カメラの光軸はスクリーンの中心を通り、水平方向の視野角θw[°]、ピクセル数は横w[px]、縦h[px]であるとします。

（上の透視変換とまとめてスクリーン変換と呼ばれている場合もあります）

[latex]\left( \begin{matrix} u \\ v \end{matrix} \right) = \left( \begin{matrix} \frac{w}{2*\tan\frac{\theta_w}{2}} & 0 \\ 0 & \frac{w}{2*\tan\frac{\theta_w}{2}} \\ \end{matrix} \right) \left( \begin{matrix} x \\ y \end{matrix} \right) + \left( \begin{matrix} w/2 \\ h/2 \end{matrix} \right)[/latex]

２．ワールド座標 → スクリーン座標への変換

空間内のある位置に存在している点が、カメラで撮影した画面のどこに対応するのかを計算する方法を説明します。2ステップに分かれています。

ワールド座標 → カメラ座標（視野変換、ビューイング変換）

ワールド座標系において座標(x, y, z)に存在する点が、カメラの座標系においてどの座標(x', y', z')に位置するかを求めます。カメラは、原点が位置t=(tx, ty, tz)にあり回転行列Rで表される方向に各軸が向いているものとします。

これは、上の座標変換で計算したように、位置の平行移動分を引き、回転の逆行列をかけることで求められます。

[latex]\left( \begin{matrix} x' \\ y' \\ z' \end{matrix} \right) = R^{-1} \left( \left( \begin{matrix} x \\ y \\ z \end{matrix} \right) - \left( \begin{matrix} t_x \\ t_y \\ t_z \end{matrix} \right) \right)[/latex]

カメラ座標 → スクリーン座標（透視投影）

カメラ座標系で座標(x', y', z')の点に対応する、スクリーン座標における座標(u, v)を求めます。これは、透視変換とスクリーン変換をあわせて以下のようになります。

[latex]\left( \begin{matrix} u \\ v \end{matrix} \right) = \left( \begin{matrix} \frac{w}{2\tan\frac{\theta_w}{2}} & 0 \\ 0 & \frac{w}{2\tan\frac{\theta_w}{2}} \\ \end{matrix} \right) \left( \begin{matrix} x'/z' \\ y'/z' \end{matrix} \right) + \left( \begin{matrix} w/2 \\ h/2 \end{matrix} \right)[/latex]

３．スクリーン座標 → ワールド座標への変換

正確にいうとスクリーン座標(u, v)からだけでは、ワールド座標への変換はできません。なぜなら、(u, v)だけではどの奥行きの点かわからないためです。ここでは変換したい点の奥行きをzとして計算していきます（例えば、Depth画像を利用して奥行きを取得することができます）。基本的には、上の計算の逆をたどっていく形になります。

カメラの設定は上と同じです。

スクリーン座標 → カメラ座標（透視投影の逆）

スクリーン座標(u, v, z)から、カメラ座標系における座標(x', y', z')への変換は以下のようです。

[latex]z'=z[/latex]

[latex]\left( \begin{matrix} x' \\ y' \end{matrix} \right) = z \left( \begin{matrix} \frac{2\tan\frac{\theta_w}{2}}{w} & 0 \\ 0 & \frac{2\tan\frac{\theta_w}{2}}{w} \\ \end{matrix} \right)\left( \left( \begin{matrix} u \\ v \end{matrix} \right) - \left( \begin{matrix} w/2 \\ h/2 \end{matrix} \right) \right)[/latex]

カメラ座標 → ワールド座標（視野変換、ビューイング変換の逆）

カメラ座標系からワールド座標系への変換は以下のようです。

[latex]\left( \begin{matrix} x \\ y \\ z \end{matrix} \right) = R \ \left( \begin{matrix} x' \\ y' \\ z' \end{matrix} \right) + \left( \begin{matrix} t_x \\ t_y \\ t_z \end{matrix} \right)[/latex]