![[Python][Scikit-learn]主成分分析を用いた次元削減、主成分ベクトルを用いた予測と線形回帰による予測の比較](https://devio2023-media.developers.io/wp-content/uploads/2016/02/eye-catch-statistics.png)
[Python][Scikit-learn]主成分分析を用いた次元削減、主成分ベクトルを用いた予測と線形回帰による予測の比較
この記事は公開されてから1年以上経過しています。情報が古い可能性がありますので、ご注意ください。
はじめに
主成分分析はデータ分析において、対象となるデータの説明変数を減らし、後に続く予測の際の計算量を削減するなどします。 本記事ではScikit-learnを用いて以前の線形回帰の記事, 線形重回帰の記事で取り上げたデータを題材とし、主成分分析を用いた次元削減を行います。 普段私達が馴染んでいる2次元空間での図をもとに、主成分分析が何をやっているか図解しながら見ていければと思います。
主成分分析
主成分分析は既存のデータの次元数を削減する手法として知られ、データの次数を削減することによって、次元の呪いを回避できることがあります。
この次元の呪いとはデータの次元数が多くなるにしたがって、データの取得や分析の際にあらわれる現象のことを指しており、分析、予測の際の計算時間の増大やデータが疎(空間上でまばら)になることをもたらします。
計算時間の増大は計算資源を投入すれば対処はある程度できると考えられますが、データが疎であることは特定の分析手法が適用できないことにもつながります。
例えば、はじめてのパターン認識の第五章ではk最近傍法を用いる際に次元の呪いが原因となって、この分析手法が前提としている仮定が成り立たないケースが解説されています。
このため、次元数が多いデータセットについては前処理として主成分分析を行い、次元の削減の可能性を検討する余地があるといえます。
主成分分析は数学的には、学習データの分散が大きくなる方向への線形変換を求める手法です。まず数式てんこ盛りにする前に、過去の記事で線形単回帰で求めた図を例に考えてみます。
図によるざっくりとした理解
2次元のデータ
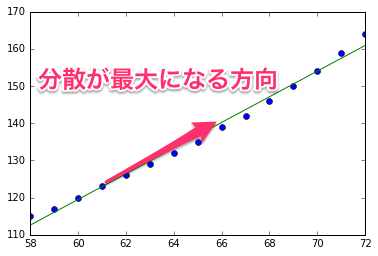
この図は単回帰モデルの結果を元に作られています。単回帰モデルのため入力がx軸にありますが、xy平面上の点を入力として考えてみると、主成分分析の問題になります。主成分分析によって求められた分散の方向を用いて、あたかも二次元平面上の各点が分散が大きくなる方向を表すベクトルを使った次のような直線付近にあるとみなせます。
[latex] \left( \begin{array}{ccc} x \\ y \end{array} \right) = a \boldsymbol{u} + \boldsymbol{c} [/latex]
(ここで \( \boldsymbol{c} \) は定数ベクトル)このデータ・セットに対しては \(\boldsymbol{u}\) が主成分分析で求められるというわけです。
数学的側面
主成分分析の一般的な数学的側面にふれてみます。学習データを
[latex] \boldsymbol{x}_i = \left( x_{i1}, \dots, x_{id} \right) ^ T (i = 1, \dots , N) [/latex]
データ行列を \( \boldsymbol{X} = \left( \boldsymbol{x}_i, \dots , \boldsymbol{x}_N \right)^T \) 、原点を平均としたデータ行列を \( \bar{ \boldsymbol{X} } = ( \boldsymbol{x}_i - \bar{ x }, \dots , \boldsymbol{x}_N - \bar{ x } )^T \) としたとき( \( \bar{x} \) は学習データの平均)、次のように定義された共分散行列
[latex] \boldsymbol{S} = \frac{1}{N} \bar{ \boldsymbol{X} } ^ T \boldsymbol{X} [/latex]
に対して固有ベクトル(正規化済み)を求めます。
[latex] \boldsymbol{S} \boldsymbol{u}_i = \lambda_i \boldsymbol{u}_i [/latex]
この固有ベクトル \( \boldsymbol{u}_i \) に対応する固有値 \( \lambda_i \) は式変形によって各ベクトルに対応する分散とみなせ、この分散が大きくなる固有ベクトルを用いて先ほどの図のような平面や方向を決定できます。
またこれら固有値の総和 \( V_{\text{total}} = \sum^d_{i = 1} \lambda_i \) は、もともとのデータの全分散量と一致します。
\(\lambda_1, \dots , \lambda_d \) を固有値の大きい順に数えて \(s_1, \dots , s_d \) とし固有ベクトルをそれに応じて並べ替えた上で、並べ替え後の第k番目の固有ベクトルに対応する成分を主成分分析では第k成分と呼んだりします。
第k成分に対応する固有値を全分散量で割ったものは寄与度と呼ばれ、第k成分がデータの説明にどれだけ寄与しているか示しています。
[latex] c_k = \frac{s_k}{V_{\text{total}}} [/latex]
データ・セット
線形単回帰の記事, 線形重回帰モデルの記事と同様に今回も米国女性の平均身長と平均体重のデータ・セット、オゾン量のデータセットを用います。
Scikit-learn
Scikit-learnはPythonの機械学習ライブラリです。あくまで主成分分析はこのライブラリの機能のなかの一部で、他にも下記のような様々な分析用途向けにアルゴリズムを提供しています。
- 分類(Classification)
- 回帰(Regression)
- クラスタリング(Clustering)
- 次元削減(Dimensionality reduction)
- モデル選別(Model selection)
- 前処理(Preprocessing)
今回はこのうちの次元削減の分析用途の中にある主成分分析向けのクラス sklearn.decomposition.PCA を用います。
線形単回帰で用いたデータを主成分分析してみる
まずは線形単回帰で用いたデータに対して主成分分析してみましょう。いつものようにソースコードはGithub上にあります。 前回記事と処理の概要は大方変わらないので、主成分分析に関わる箇所のみ解説していきます。
In [1]:
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.decomposition import PCA
%matplotlib inline
datum = np.loadtxt("women.tsv", delimiter="\t", usecols=(1, 2), skiprows=1)
weights = np.transpose(datum)[0]
heights = np.transpose(datum)[1]
- l4 :
sklearn.decompositionモジュールのPCAクラスをインポートします。
In [2]:
pca = PCA(n_components = 1) pca.fit_transform(np.transpose(np.array([weights, heights])))
- l1 : PCAクラスのインスタンスを主成分の個数を引数として生成します。
- l2 :
fit_transformメソッドで引数に渡されたデータの主成分分析を行います。引数データの形状は(サンプル数, 説明変数の個数)を持ちます。
この fit_transform 関数の返り値として主成分分析を行い、サンプル全体の中心からどの程度個々のサンプルが離れているかを成分に掛ける係数を用いて表します。式で書くなら、主成分分析で得られた第k主成分を表すベクトルを \( \boldsymbol{p}k \) 、そのそれぞれに各サンプル \( \boldsymbol{x}_i \) を説明するために掛ける係数を \( f{ik} \) として下記のように各サンプルは表わせます。
[latex] \boldsymbol{x}_i = \sum^n_{k = 1} f_{ik} \boldsymbol{p}_k + \bar{ \boldsymbol{x} } [/latex]
この中の \( f_{ik} \) で作られる行列がこのメソッドの返り値になるようです。ここでは主成分として一つのみを仮定しているため、列数1の行列が得られます。
Out [2]:
array([[-22.82135677],
...
[ 28.13934705]])
In [3]:
pca.get_covariance()
get_covariance()メソッドで対象となるデータの共分散行列を得ます。
Out [3]:
array([[ 18.66666667, 64.4 ],
[ 64.4 , 224.19555556]])
In [4]:
pca.explained_variance_ratio_
explained_variance_ratio_属性で成分毎の寄与率を求められます。一つの成分しか仮定してませんが、念のため出力を確認します。
Out [4]:
array([ 0.99936171])
ほぼ100%の寄与率のようです。
In [5]:
s = pca.components_[0] s
components_属性で主成分を表すベクトルの配列が得られます。その0番目を取ることで第一主成分の向きを確認します。
Out [5]:
array([ 0.27626124, 0.96108258])
In [6]:
実際に得られた主成分の向きを確認するために、データとともに図にプロットしてみましょう。
plt.plot(weights, heights, "o") plt.plot(weights, np.mean(heights) + s[1] / s[0] * (weights - np.mean(weights)), "g") plt.show()
- l2 : のグラフにプロットしている式
np.mean(heights) + s[1] / s[0] * (weights - np.mean(weights))は下記から導けます
[latex] \left( \begin{array}{ccc} x \\ y \end{array} \right) = f \boldsymbol{s} + \left( \begin{array}{ccc} \bar{x} \\ \bar{y} \end{array} \right) [/latex]
\(\bar{x}\) が np.mean(weights), \(\bar{y}\) が np.mean(heights) に対応しています。
このコードの実行によって下記の図が生成されます。
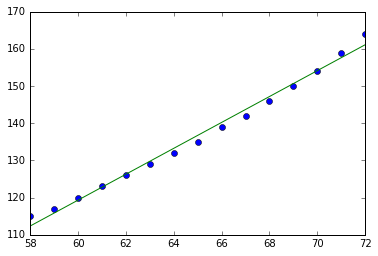
第一主成分の方向は分散の最大になる方向になっていることがうかがえますね!
In [7]:
また、線形単回帰で作成したモデルも下記のコードによって重ねてみましょう。
alpha = -87.43 beta = 3.45 fig = plt.figure() plt.plot(weights, heights, "o") plt.plot(weights, np.mean(heights) + s[1] / s[0] * (weights - np.mean(weights)), "g") plt.plot(weights, alpha + beta * weights, "r") plt.show()
- l1, 2: これらの係数は前回記事の単回帰モデルから導かれたものです。
- l7 : 線形単回帰モデルのプロットを赤い線で出力します。
このコードの実行によって下記の図が生成されます。
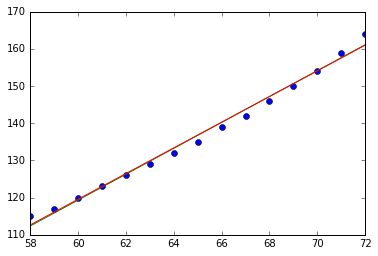
このデータに関する結論
線がぴったりと重なっています!身長と体重のデータについては一次元的な量で記述できると考えて良さそうです。
線形重回帰で用いたデータを主成分分析してみる
次に線形重回帰で用いたデータに対して主成分分析してみましょう。ソースコードはGithub上にあります。前処理の流れや、主成分分析の部分は前回記事や、単回帰の時とほぼおなじですので主要な部分のみ見ていきます。なお、今回のデータについては2つの主成分を取ると仮定してPCAクラスのインスタンスを生成しています。
In [6]:
下記のコードで各主成分の寄与率が視覚的に確認するためのスクリーンプロットを生成します。
plt.bar([1, 2], pca.explained_variance_ratio_, align = "center")
plt.title("Screeplot")
plt.xlabel("components")
plt.ylabel("contribution")
plt.show()
- l1 : 各主成分の寄与率をバー状の図で生成します。
下記の図が生成されます。
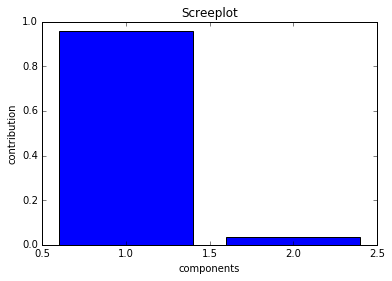
第一成分の寄与度が高く、全体として一次元的なデータになっていることが伺えます。
In [8]:
下記のコードで主成分の方向とデータ・セットをプロットしてみます。また、同時に前回作成した重回帰モデルで作られる平面もプロットし、主成分の方向と比較してみます。
from mpl_toolkits.mplot3d import Axes3D
coeff = 40
beta_0 = -67.24
beta_wind = -3.29
beta_temp = 1.83
def show_with_angle(angle):
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.view_init(elev = 10., azim = angle)
ax.set_zlim(0, 150)
x = np.arange(0, 20, 0.5)
y = np.arange(60, 100, 1.0)
X, Y = np.meshgrid(x, y)
Z = beta_0 + beta_wind * X + beta_temp * Y
surf = ax.plot_surface(X, Y, Z, rstride = 5, cstride = 5, alpha = 0.4)
ax.plot([np.mean(winds), np.mean(winds) + coeff * u[0]], [np.mean(temps), np.mean(temps) + coeff * u[1]], [np.mean(ozones), np.mean(ozones) + coeff * u[2]], 'r')
ax.plot([np.mean(winds), np.mean(winds) + coeff * v[0]], [np.mean(temps), np.mean(temps) + coeff * v[1]], [np.mean(ozones), np.mean(ozones) + coeff * v[2]], 'c')
ax.scatter(winds, temps, ozones, c='green', marker='o', alpha=1)
ax.set_xlabel('Wind')
ax.set_ylabel('Temp')
ax.set_zlabel('Ozone')
plt.show()
for angle in range(-120, 120, 30):
show_with_angle(angle)
- l3 : 主成分の方向を表示するために掛ける係数です。図をみやすくするために置いたもので、特に分析結果等に絡むものではないです。
- l4-6 : 前回作成した重回帰モデルのパラメータ係数です。
- l18, 19 : 主成分の方向を確認するための線分をプロットしています。第一主成分が赤、第二主成分がシアンです。
これらのコードで下記の図が出力されます。
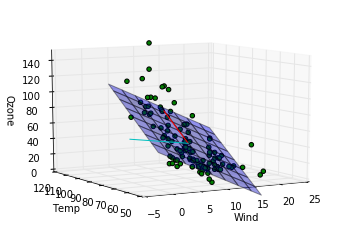
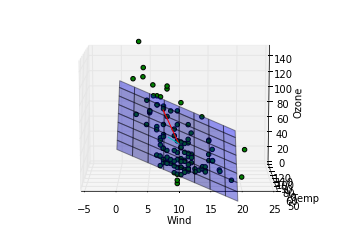
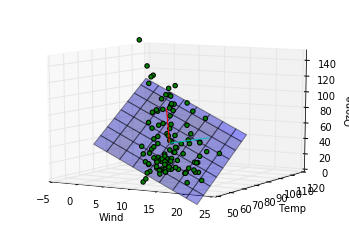
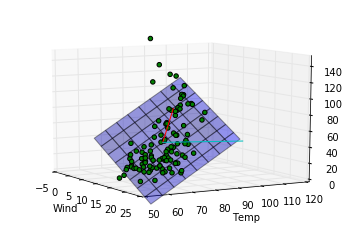
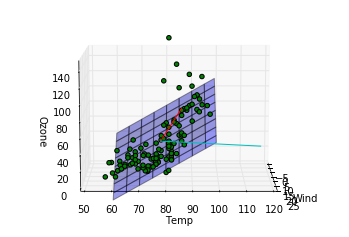
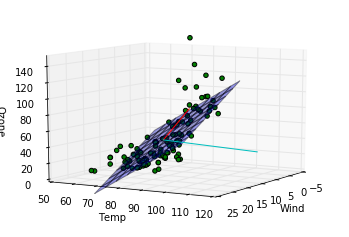
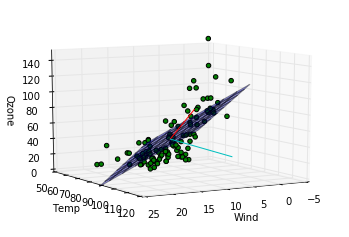
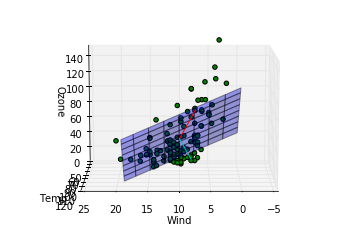
このデータに関する結論
第一主成分の方向は重回帰モデルによってはじき出された平面に近い方向をむいていますが、第二成分は寄与度が少ないせいか、重回帰モデルの平面とは関係のない方向を向いていることがわかります。主成分分析によって得られる成分は必ずしも重回帰モデルで得られる平面を表す成分とは一致しないことがわかりました。重回帰の時にはオゾン量が風量、温度の二成分で説明できるという仮定をしましたが、もっと大胆な仮定、つまり特定の風量と温度を持つ一成分のみでオゾン量が記述できるという仮定をおけるかもしれないです。
記事内容に関連する手法
因子分析
主成分分析によって求められた各主成分に対しての解釈をやりやすくするため、主成分分析の結果から主成分の方向を表すベクトルを集めて行列とし、それに回転を加えて、もともとの説明変数で説明できるようなわかりやすい結果にする方法です。回転方法としてよく用いられる方法としてバリマックス回転という方法があるようです。アンケート調査や心理学分野の分析としてよく聞く手法です。
部分空間法
クラス分けされたデータに対しての主軸(寄与度の高い成分で作られる座標軸)を共分散行列や相関行列を用いて求め、与えられたデータに対してどの主軸の成分が大きいかを判断することでデータを分類する手法です。クラスのデータのみを利用すればそのクラスの部分空間を構成でき、識別器として利用できる点が優れています。
まとめ
今回はデータ・セットに対する次元削減の手段として主成分分析を紹介し、前回の線形回帰の方法と比較しました。いかがでしたでしょうか。 次元削減については他にも様々な手法があり、朱鷺の杜に興味深いまとめがありました。そちらに紹介されている手法も今後試していければと思っています。







