画像の座標を空間の座標に変換する
この記事は公開されてから1年以上経過しています。情報が古い可能性がありますので、ご注意ください。
カフェチームの山本です。
現在カフェチームでは、カメラから取った映像に映っているユーザの骨格や手の位置を検出し、そのユーザがどの商品を取ったかを認識することに取り組んでいます。画像処理によって、関節など(Landmark)が画像上のどこに位置しているのかはわかりますが、実際の空間においてどの位置に存在するかは直接はわかりません。(そのため、例えば、棚に置かれたどの商品を取ったかを判定する、といったことができません。)
前回は、基本的な座標変換と、ワールド座標系とスクリーン座標系との間の変換について調べました。
今回は、画像上の位置(+奥行き)から、実際の空間における位置に変換するため、行列を利用した計算方法をまとめ、コードを実装しました。また、テストとして3DCG(UnrealEngine)を利用しました。空間に配置したオブジェクトを撮影し、その画像内の座標とデプスから、もとの座標に変換できることを確認しました。
今回と異なる定義を用いている説明もありますので、混乱されないようご注意ください。(複雑、、、)
お詫び
本ページの数式が正しく表示されていません。現在、修正中です。数式まで見たい方はこちらのページをご覧ください。
0.用語の定義
説明にあたって、利用する用語を定義しておきます。
基礎用語
- 座標系:原点と軸のセット。
- 基底(ベクトル):座標系の各軸の方向を向き、長さ1のベクトル。またはそのセット。
- 位置:空間(平面)中の位置。
- 座標:空間中の位置を、座標系における基底ベクトルの線形和で表現したもの。空間中の同じ位置であっても、座標系によって座標が変わります。
- 回転:座標系の軸における回転。右手系の場合、軸が正となる方向から原点を向いて、左回り(反時計周り)が正です。
- 右手(直交座標)系:下図のように、x軸・y軸・z軸の相対関係が右手の親指・人差し指・中指の向きのようになっています。
- 左手(直交座標)系:下図のように、x軸・y軸・z軸の相対関係が左手の親指・人差し指・中指の向きのようになっています。

左:左手系 右:右手系
画像は https://ja.wikipedia.org/wiki/右手系 より
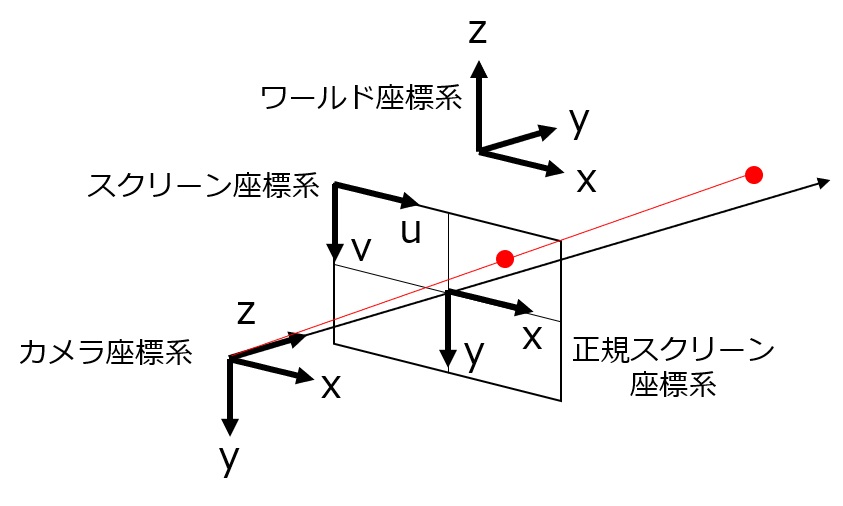
変換する座標系

- ワールド座標系:基準となる座標系。今回は右手系とします。
- カメラ座標系(ビュー座標系):実際の空間に存在するカメラの位置を原点として、注視する方向にz軸、z軸に垂直な面における右方向をx軸、下方向をy軸とした座標系。
- 正規スクリーン座標系:カメラ座標系からみた位置を、z=1の平面に透視投影した際の、平面における座標。z軸との交点を原点として、x軸とy軸が元のカメラ座標系と同じ方向。
- スクリーン座標系:正規スクリーン座標系を、カメラで撮影した場合の座標に変換したもの。スクリーンの大きさの1/2分、原点が左上のずれている。画面右方向をu軸(x軸)、下方向をv軸(y軸)とする。また、カメラ座標系のz軸を、スクリーン座標系のz軸とする。u軸(x軸)とv軸(y軸)の単位はピクセル数、z軸の単位はワールド座標と同じです。
1.状況の整理
想定

今回は、以下のような状況を想定しています。
- カメラでRGBイメージとDepthイメージを取得する
- RGBイメージから骨格の座標を検出する(u, v)
- Depthイメージにおける骨格の位置の値を取得する(z)
- スクリーン座標(u, v)+ zを変換し、ワールド座標系における座標(x, y, z)を得る
入出力
入力は以下です。
- カメラのワールド座標系における位置・回転行列 = t, R
- カメラの内部パラメータ行列 = K
- RGB画像上の(スクリーン座標系における)座標 = (u, v)
- Death画像における(=スクリーン座標系における)奥行き = z
出力は以下です。
- 実際の空間(ワールド座標系)における座標 = (x', y', z')
計算
数式としては、以下のようになります。
[latex]\left( \begin{matrix} x' \\ y' \\ z' \end{matrix} \right) = R K^{-1} z \left( \begin{matrix} u \\ v \\ 1 \end{matrix} \right) + t[/latex]
2.コードの実装
今回はPythonを利用して、以下のように実装しました。
import numpy as np
def convert_uvz_to_xyz(u, v, z, R, t, K):
K_inv = np.linalg.inv(K)
# in screen coord
cs = np.asarray([u, v, 1])
cs_ = cs * z
# in camera coord
cc = np.dot(K_inv, cs_)
# in world coord
cw = np.dot(R, cc) + t
return cw
3.動作の確認
前準備:座標系の修正
動作を確認するため、3DCGを利用しました。今回利用したソフトウェアはUnrealEngineです。UnrealEngineの座標系は今までの座標系とは異なり、奥方向をx軸(xu)、右方向をy軸(yu)、上方向をz軸(zu)としている左手系です。デフォルトのカメラの位置は原点で、x軸が右方向、y軸が下方向、z軸が奥行き方向になっている右手系です。回転は通常の右手系と同様です.

UnrealEngineの座標系をワールド座標に変換するために、以下のように計算します。UnrealEngine空間のyu軸をx軸に、zu軸の逆方向をy軸に、xu軸方向をz軸に変換します。回転については、修正する必要はありません。
import numpy as np
R_unreal_to_world = np.asarray([
[0, 1, 0],
[0, 0, -1],
[1, 0, 0],
])
def convert_coord_unreal_to_world(cu):
# coord in world
cw = np.dot(R_unreal_to_world, cu)
return cw
def convert_coord_world_to_unreal(cw):
R_unreal_to_world_inv = np.linalg.inv(R_unreal_to_world)
# coord in unrealengine
cu = np.dot(R_unreal_to_world_inv, cw)
return cu
用意したデータ
確認用に、以下のようなデータを用意しました。半径の長さ5の球が、12個等間隔に並んでいる空間を、カメラで撮影しました。画像・データは同じカフェチームの宮島が作成しました。スクリーン座標のx・yは、画像に写った各球の一番上の点を目視で計測し(1ピクセル単位)、奥行きはUnrealEngineを利用して取得しました。UnrealEngine座標は、各球の中心の座標です。(そのため、球の半径分ずれています。)

# UnrealEngine座標系におけるカメラの座標
cam_coord = [392, 336, 234]
# カメラの回転角度(カメラ座標におけるx軸、y軸、z軸での回転)
cam_rot = [326, 41, 0]
# カメラの視野角(水平方向)
fov = 90
# スクリーンの画素数(横)
pw = 1280
# スクリーンの画素数(縦)
ph = 720
# カメラ情報(内部パラメータ)
cam_info = (fov, pw, ph)
# 対応する座標の組み合わせ
# uvz(スクリーン座標+Depth), xyz(UnrealEngine座標) の順
coord_set = [
([663, 306, 263], [560, 500, 100]),
([776, 366, 227], [500, 500, 100]),
([935, 453, 189], [440, 500, 100]),
([758, 263, 297], [560, 560, 100]),
([871, 313, 258], [500, 560, 100]),
([1022, 376, 222], [440, 560, 100]),
([661, 402, 291], [560, 500, 50]),
([762, 469, 255], [500, 500, 50]),
([898, 562, 218], [440, 500, 50]),
([748, 354, 324], [560, 560, 50]),
([849, 408, 287], [500, 560, 50]),
([978, 481, 250], [440, 560, 50]),
]
変換処理
まず計算に必要な行列などを計算します。
import numpy as np
from numpy import sin, cos, tan
def calc_R(pitch, yaw, roll):
a = np.radians(pitch)
b = np.radians(yaw)
c = np.radians(roll)
R_x = np.asarray([
[1, 0, 0],
[0, cos(a), -sin(a)],
[0, sin(a), cos(a)],
])
R_y = np.asarray([
[cos(b), 0, sin(b)],
[0, 1, 0],
[-sin(b), 0, cos(b)],
])
R_z = np.asarray([
[cos(c), -sin(c), 0],
[sin(c), cos(c), 0],
[0, 0, 1],
])
R = np.dot(R_z, np.dot(R_y, R_x))
return R
def calc_K(fov_x, pixel_w, pixel_h, cx=None, cy=None):
if cx is None:
cx = pixel_w / 2.0
if cy is None:
cy = pixel_h / 2.0
fx = 1.0 / (2.0 * tan(np.radians(fov_x) / 2.0)) * pixel_w
fy = fx
K = np.asarray([
[fx, 0, cx],
[0, fy, cy],
[0, 0, 1],
])
return K
def calc_t(camera_coord):
return convert_coord_unreal_to_world(camera_coord)
t = calc_t(cam_coord)
R = calc_R(*cam_rot)
K = calc_K(*cam_info)
座標変換を実行するコードは以下のようです。
for cs, cu in coord_set:
u, v, z = cs
# 変換によって推定したワールド座標系での座標
cw_ = convert_uvz_to_xyz(u, v, z, R, t, K)
# ワールド座標をUnrealEngine座標に変換する
cu_ = convert_coord_world_to_unreal(cw_)
print(cs)
print(cu_)
print(cu)
print()
結果
変換結果は以下のようになりました。データの説明で述べたように球の半径分ずれているものの、正しく変換できていることがわかります。
[663, 306, 263] [559.7188109 494.31918112 105.32912827] [560, 500, 100] [776, 366, 227] [501.48517357 495.08932364 105.29891533] [500, 500, 100] [935, 453, 189] [441.50938365 494.46925599 105.54380154] [440, 500, 100] [758, 263, 297] [560.89955496 555.37902653 105.23805678] [560, 560, 100] [871, 313, 258] [500.32877983 553.55646597 105.43590216] [500, 560, 100] [1022, 376, 222] [441.62735839 554.71290743 105.2580169 ] [440, 560, 100] [661, 402, 291] [559.74987692 494.47454703 55.4428382 ] [560, 500, 50] [762, 469, 255] [501.32988858 495.44707566 55.40096691] [500, 500, 50] [898, 562, 218] [441.70533822 495.65198943 55.05298057] [440, 500, 50] [748, 354, 324] [560.13304525 554.60091183 55.3397009 ] [560, 560, 50] [849, 408, 287] [500.99864044 554.93584504 55.66660295] [500, 560, 50] [978, 481, 250] [441.85292732 554.27961034 55.01679512] [440, 560, 50]
まとめ
今回は、撮影した画像における点+奥行きが、空間のどの位置に当たるのかを計算する方法を考えました。また、3DCGを利用して、正しく座標を変換できることを確認しました。これによって、骨格検出などで検出した手の位置がわかるため、手にとった商品の棚を判別する、といったことができそうです。










