カメラの外部パラメータ行列を最小二乗法で推定する
この記事は公開されてから1年以上経過しています。情報が古い可能性がありますので、ご注意ください。
カフェチームの山本です。
現在、カフェチームでは、機械学習を用いて、画像内に映っている人物の骨格や手を検出することで、どの商品を取り出したかを判定する方法を検討しています。
前回は、RGB画像から骨格検出した特徴点の、画像における座標座標(=スクリーン座標)と、Depth画像から取得した値(=奥行き)から、空間内の座標(=ワールド座標、ToF座標)に変換する方法を検討しました。ただし、この方法では、カメラの位置や回転(=外部パラメータ)は予めわかっている必要がありました。
今回は、実際にカメラの位置や回転を計測することなく、この外部パラメータを推定する方法を考えます。方法としては、予め同じ位置の点に対して、「スクリーン座標+奥行き」と「ワールド座標」を計測し、最小二乗法によってカメラの外部パラメータの行列を推定します。
本記事と異なる定義を用いている説明もありますので、混乱されないようご注意ください。正直なところ、解説する方ごとに定義が異なっていたり、目的どおりの計算が載ってなかったりと、かなり難しかったです。備忘録としてまとめていますが、間違っているところがあったら、コメント等でお教えいただけると大変助かります!
お詫び
本ページの数式が正しく表示されていません。現在、修正中です。数式まで見たい方はこちらのページをご覧ください。
0.概要
今回やりたいこと
空間における座標(=ワールド座標)と、画像における座標(スクリーン座標)とを変換するには、カメラがどの位置にあり、どの方向を向いているかの情報(=外部パラメータ行列)と、カメラがどの程度ズームしていて、どの程度の解像度で撮影しているかの情報(=内部パラメータ行列)がわかっている必要があります。
前回の方法では、カメラの外部パラメータ(=[R|t])は予めわかっているものとして、計算を考えました。そのため、実際の場面でカメラを設置して座標変換を行う場合、空間内のどの座標にカメラがあるか、どの方向を向いているか計測する作業が必要であり、大変時間がかかります。また、測定した値で計算しても誤差が大きい場合などは、補正のための計算を追加する必要があり、大変不便です。
今回の方法は、実際にカメラの位置や回転を計測することなく、この外部パラメータを推定する方法を考えます。方法としては、同じ位置の点に対して、キャリブレーション用データとして「スクリーン座標+奥行き」と「ワールド座標」のセットを用意し、最小二乗法によって、外部パラメータ行列を推定します。
今回の方法では、内部パラメータは既知であるものとします。内部パラメータも同時に推定する方法もありますが、今回の記事からは範囲外です。内部パラメータは、ズームや解像度、カメラの設定値なので、設置後に頻繁に変えることは(基本的には)ないと思われます。
復習:座標変換の計算
詳しくは前々回の記事を見ていただきたいのですが、「スクリーン座標+奥行き」と「ワールド座標」には、以下のような関係があります。
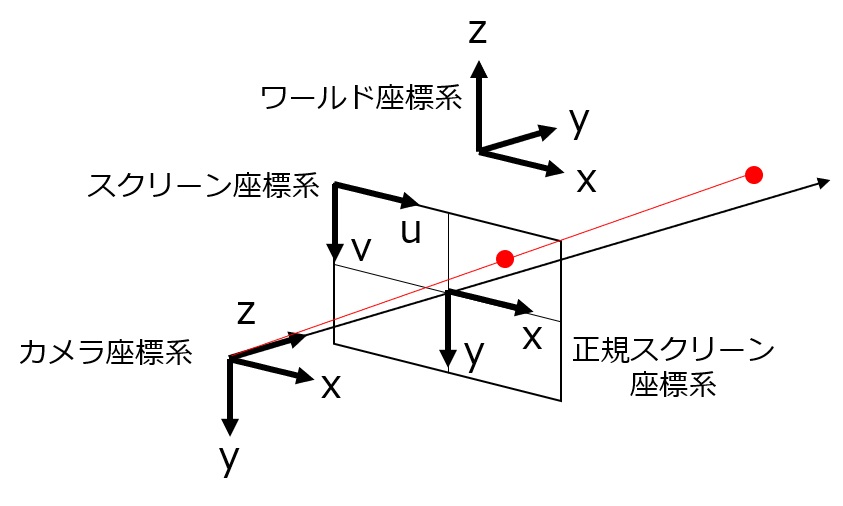
tはスクリーン座標系におけるカメラの並進ベクトル、Rはスクリーン座標系におけるカメラの回転行列、Kはカメラの内部パラメータ行列、cwはワールド座標系における座標、ccはカメラ座標系における座標、(us, vs)はスクリーン座標系における座標、zsはカメラから見た奥行きを表します。
[latex]R = \left( \begin{matrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \end{matrix} \right)[/latex]
[latex]t=\left( \begin{matrix} t_{1} \\ t_{2} \\ t_{3} \end{matrix} \right)[/latex]
[latex]K = \left( \begin{matrix} f_{w} & 0 & c_{x} \\ 0 & f_{h} & c_{y} \\ 0 & 0 & 1 \end{matrix} \right)[/latex]
[latex]c_{w} =\left( \begin{matrix} x_{w} \\ y_{w} \\ z_{w} \end{matrix} \right)[/latex]
[latex]c_{c} =\left( \begin{matrix} x_{c} \\ y_{c} \\ z_{c} \end{matrix} \right)[/latex]
[latex]c_{w} = \left[ R | t \right] \left( \begin{matrix} c_{c} \\ 1\end{matrix} \right)[/latex]
[latex]c_c = z_s K^{-1} \left( \begin{matrix} u_s \\ v_s \\ 1 \end{matrix} \right)[/latex]
書き直すと、以下のようになります。
[latex]\left( \begin{matrix} x_c \\ y_c \\ z_c \end{matrix} \right) = z_s K^{-1} \left( \begin{matrix} u_s \\ v_s \\ 1 \end{matrix} \right)[/latex]
[latex]\left( \begin{matrix} x_w \\ y_w \\ z_w \end{matrix} \right) = \left[ \begin{matrix} r_{11} & r_{12} & r_{13} & t_{1} \\ r_{21} & r_{22} & r_{23} & t_{2} \\ r_{31} & r_{32} & r_{33} & t_{3} \end{matrix} \right] \left( \begin{matrix} x_c \\ y_c \\ z_c \\ 1 \end{matrix} \right)[/latex]
右辺の第1項が(今回推定したい)カメラの外部パラメータ行列です。
1.計算:外部パラメータの推定
推定用データ
今回利用するデータは以下の2つです。
カメラの内部パラメータ行列
先程述べたように、今回は既知であるとします。例えば、カメラの画角とピクセル数から計算できます。スクリーン座標をカメラ座標に変換するために使用します。
予め計測したcwと(us, vs, zs)
同じ位置の点を、カメラ画像から検出したスクリーン座標+奥行きと、ワールド座標で表した座標の組み合わせです。以下のような、対応関係が得られたものとします。
[ ([xw0, yw0, zw0], [us0, vs0, zs0]), ([xw1, yw1, zw1], [us1, vs1, zs1]). ... ]
先程の式を利用して、スクリーン座標(us, vs, zs)をカメラ座標(xc, yc, zc)に変換しておきます。これによって、ワールド座標とカメラ座標の対応関係が得られます。
[latex]\left( \begin{matrix} x_c \\ y_c \\ z_c \end{matrix} \right) = z_s K^{-1} \left( \begin{matrix} u_s \\ v_s \\ 1 \end{matrix} \right)[/latex]
[ ([xw0, yw0, zw0], [xc0, yc0, zc0]), ([xw1, yw1, zw1], [xc1, yc1, zc1]). ... ]
計算方法:考え方
得られた対応関係をもとに、以下のように考えることができます。
[latex]B = \left( \begin{matrix} x_{w0} & y_{w0} & z_{w0} \\ x_{w1} & y_{w1} & z_{w1} \\ & \vdots & \end{matrix} \right)[/latex]
[latex]A = \left( \begin{matrix} x_{c0} & y_{c0} & z_{c0} & 1 \\ x_{c1} & y_{c1} & z_{c1} & 1 \\ & \vdots & \end{matrix} \right)[/latex]
[latex]\begin{matrix} X &=& \left[R|t \right]^{T}\\ &=& \left( \begin{matrix} R^{T} \\ t^{T} \end{matrix} \right) \\ &=&\left( \begin{matrix} r_{11} & r_{21} & r_{31} \\ r_{12} & r_{22} & r_{32} \\ r_{13} & r_{23} & r_{33} \\ t_{1} & t_{2} & t_{3} \end{matrix}\right) \end{matrix}[/latex]
としたとき、
[latex]\left| B - A X \right| \rightarrow \min[/latex]
をとなるXを最小二乗法で求める。
これによって、すべての点における「ワールド座標に変換した座標の誤差の2乗」の和を最小にするX(=外部パラメータ行列の転置行列)を求めることができます。
(少しわかりにくいですが、式としては、データのcwと[R|t]ccを転置して縦にならべています。)
結論:Xの求め方
証明や説明は少しむずかしいので、先に結論を述べます。上を満たすXの解は、以下のようにして求められます。
[latex]\hat{X}=\left(A^{T}A\right)^{-1}A^{T}B[/latex]
自分で上の計算していってXを求めることもできますが、Pythonのnumpy.linalg.lstsqを利用すると、AとBから直接Xを求められます。(実際のコードは次節のとおりです)
2.動作確認
用意したデータ
前回利用したものと同じく、UnrealEngineで作成したデータです。
画像の座標を空間の座標に変換する | Developers.IO
数値としては、以下のようなものです。データの12点のうち、8点(coord_set_for_estimation)を外部パラメータ行列の推定に利用して、残りの4点(coord_set)で変換結果を確認しました。
実装(Python、numpy)
コードとしては以下のようになります。今回の方法では、右手系左手系の変換も同時に推定できるので、UnrealEngine座標とスクリーン座標からそのまま計算できます(右手系のワールド座標系への変換は必要ありません。)
import numpy as np
from numpy import sin, cos, tan
from operator import itemgetter
# internal parameters are known
fov = 90 # horizontal
pw = 1280
ph = 720
coord_set_for_estimation = [
# uvz(screen cood), xyz(unrealengine coord)
([663, 306, 263], [560, 500, 100]),
([776, 366, 227], [500, 500, 100]),
([935, 453, 189], [440, 500, 100]),
([758, 263, 297], [560, 560, 100]),
([871, 313, 258], [500, 560, 100]),
([1022, 376, 222], [440, 560, 100]),
([661, 402, 291], [560, 500, 50]),
([762, 469, 255], [500, 500, 50]),
]
# calc internal parameter matrix
fx = 1.0 / (2.0 * tan(np.radians(fov) / 2.0)) * pw
fy = fx
cx = pw / 2.0
cy = ph / 2.0
K = np.asarray([
[fx, 0, cx],
[0, fy, cy],
[0, 0, 1],
])
# estimate external parameter matrix
screen_coords = list(map(itemgetter(0), coord_set_for_estimation))
world_coords = list(map(itemgetter(1), coord_set_for_estimation))
## convert screen coord to camera coord
K_inv = np.linalg.inv(K)
def conv_cs_to_cc(cs):
u, v, z = cs
cs_ = np.array([u, v, 1])
cc = np.dot(K_inv, cs_) * z
return [cc[0], cc[1], cc[2], 1]
# lambda cs: np.dot(K_inv, [cs[0], cs[1], 1] * cs[2]
camera_coords = list(map(conv_cs_to_cc, screen_coords))
## calc using lstsq
A = np.array(camera_coords)
B = np.array(world_coords)
(X, residuals, rank, s) = np.linalg.lstsq(A, B)
## split X to R,t
R = X[0:3].T
t_ = X[3:4][0]
t = [t_[0], t_[1], t_[2]]
print(R)
print(t)
# check conversion with estimated matrix
coord_set = [
# uvz(screen cood), xyz(unrealengine coord)
([898, 562, 218], [440, 500, 50]),
([748, 354, 324], [560, 560, 50]),
([849, 408, 287], [500, 560, 50]),
([978, 481, 250], [440, 560, 50]),
]
for cs, cu in coord_set:
us, vs, zs = cs
K_inv = np.linalg.inv(K)
# camera coord
cc = np.dot(K_inv, zs * np.asarray([us, vs, 1]))
# world coord (= unrealengine coord)
cw = np.dot(R, cc) + t
print(cs)
print(cu)
print(cw)
print(cu - cw)
print()
結果
上の実行結果は以下のとおりです。
# R [[-6.65033327e-01 -4.27010054e-01 6.32569825e-01] [ 7.55454130e-01 -3.72811751e-01 5.40308286e-01] [ 5.14855420e-04 -8.30778132e-01 -5.58529682e-01]] # t [389.99475776029595, 342.18082748911144, 228.4369742741566] # conversion result # screen coord, unrealengine coord, conveted coord, dif [898, 562, 218] [440, 500, 50] [440.07005911 500.70650858 49.56002197] [-0.07005911 -0.70650858 0.43997803] [748, 354, 324] [560, 560, 50] [559.88372708 559.67758245 50.02499568] [ 0.11627292 0.32241755 -0.02499568] [849, 408, 287] [500, 560, 50] [500.02169679 560.0282906 50.30471035] [-0.02169679 -0.0282906 -0.30471035] [978, 481, 250] [440, 560, 50] [440.14913559 559.38027169 49.60528321] [-0.14913559 0.61972831 0.39471679]
座標変換の結果
4点全てにおいて、誤差の絶対値が1以下になっており、精度高く変換できていそうです。
前回はデータ作成時に球の半径分間違っていたため、変換結果にもその分の誤差がのっていました。しかし、今回はその分も加味して外部パラメータを推定したため、誤差が小さくなっています。
まとめ
今回は、「スクリーン座標+奥行き」と「ワールド座標」の組み合わせから、最小二乗法によってカメラの外部パラメータ行列を推定する方法をまとめました。
これによって、カフェなどに実際に設置したカメラの位置や角度を計測する作業が不要になるため、カメラをたくさん設置できるようになりそうです。
参考にさせていただいたページ
最小二乗法の基礎をまとめる - エンジニアを目指す浪人のブログ
Numpyのlinalg.lstsqの覚書 - stMind
numpy.linalg.lstsq - NumPy v1.19 Manual
補足
最小二乗法の計算過程・証明
長くなってしまったので、別記事にまとめました。










